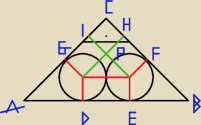
 AD = BE = x
DE = 2
AB = 2x+2
O1P = O2P = z
z2 + z2 = O1O22
2z2 = 22
2z2 = 4
z2 = 2
z = √2
AG = AD = x
GI = z = √2
IC = r = 1
AC = x + √2 + 1
BC = AC
AB2 = AC2 + BC2
(2x+2)2 = (x + √2+1)2 + (x+√2+1)2
[2(x+1)]2 = 2[ (x+1) + √2 ]2
4(x2 + 2x + 1) = 2[ (x+1)2 +2√2(x+1) + 2] /:2
2(x2 + 2x + 1) = x2 + 2x + 1 + 2√2x + 2√2 + 2
x2 + 2x − 2√2x −1 − 2√2 = 0
x2 + 2(1−√2)x − (1 + 2√2) = 0
Δ = 4(1−√2)2 + 4(1+2√2)
Δ = 4(1 − 2√2 + 2) + 4 + 8√2 = 12 − 8√2 + 4 + 8√2 = 16
√Δ = 4
AD = BE = x
DE = 2
AB = 2x+2
O1P = O2P = z
z2 + z2 = O1O22
2z2 = 22
2z2 = 4
z2 = 2
z = √2
AG = AD = x
GI = z = √2
IC = r = 1
AC = x + √2 + 1
BC = AC
AB2 = AC2 + BC2
(2x+2)2 = (x + √2+1)2 + (x+√2+1)2
[2(x+1)]2 = 2[ (x+1) + √2 ]2
4(x2 + 2x + 1) = 2[ (x+1)2 +2√2(x+1) + 2] /:2
2(x2 + 2x + 1) = x2 + 2x + 1 + 2√2x + 2√2 + 2
x2 + 2x − 2√2x −1 − 2√2 = 0
x2 + 2(1−√2)x − (1 + 2√2) = 0
Δ = 4(1−√2)2 + 4(1+2√2)
Δ = 4(1 − 2√2 + 2) + 4 + 8√2 = 12 − 8√2 + 4 + 8√2 = 16
√Δ = 4
| −2(1−√2) − 4 | −6 + 2√2 | |||
x1 = | = | = −3 + √2 < 0 | ||
| 2 | 2 |
| −2(1−√2) + 4 | 2 + 2√2 | |||
x2 = | = | = 1 + √2 > 0 | ||
| 2 | 2 |
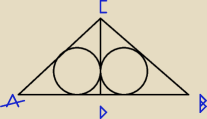 Prostszy sposób:
AD = BD = CD = a
po tr.ADCi tr.BDC prostokatne równoramienne
AC2 = a2 + a2 = 2a2
AC = BC = a√2
ObADC = 2a + a√2
Prostszy sposób:
AD = BD = CD = a
po tr.ADCi tr.BDC prostokatne równoramienne
AC2 = a2 + a2 = 2a2
AC = BC = a√2
ObADC = 2a + a√2
| a2 | ||
PADC = | ||
| 2 |
| 2P | ||
R= | ||
| Ob |
| a2 | a2 | |||
1 = | = | = U{a}{2+√2 | ||
| 2a+a√2 | a(2+√2 |
 Teraz jest ok
Teraz jest ok Dobranoc Basiu! Kolorowych snów!
Dobranoc Basiu! Kolorowych snów!
 Dobranoc. Miłych snów.
Dobranoc. Miłych snów. 
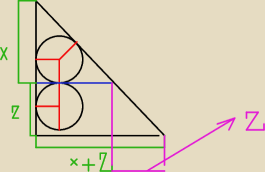 Zastanawiam się cały czas ( i nie daje mi to spokoju) czy te okręgi muszą być położone
tak jak na rysunkach (1) i (2). Wprawdzie takie położenie samo się narzuca, ale dlaczego
nie mogłoby być tak jak na rysunku (3). Mniej przekonująco wygląda, ale spełnia te same
warunki co (1) i (2).
Tam też każdy z okręgów jest styczny tylko do dwóch ramion trójkąta. Czy w takim razie
nie może być równie dobrze tak jak tu ?
Rozwiązanie jest proste bo tr. x, x, x√2 jest opisany na okręgu o promieniu r=1
Stąd liczę x.
Przeciwprostokątna = x√2 + 2√2
Ob = 2(x+2) + x√2 + √2 = 2x + 4 + x√2 + 2√2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Zastanawiam się cały czas ( i nie daje mi to spokoju) czy te okręgi muszą być położone
tak jak na rysunkach (1) i (2). Wprawdzie takie położenie samo się narzuca, ale dlaczego
nie mogłoby być tak jak na rysunku (3). Mniej przekonująco wygląda, ale spełnia te same
warunki co (1) i (2).
Tam też każdy z okręgów jest styczny tylko do dwóch ramion trójkąta. Czy w takim razie
nie może być równie dobrze tak jak tu ?
Rozwiązanie jest proste bo tr. x, x, x√2 jest opisany na okręgu o promieniu r=1
Stąd liczę x.
Przeciwprostokątna = x√2 + 2√2
Ob = 2(x+2) + x√2 + √2 = 2x + 4 + x√2 + 2√2
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
| 2P | ||
r = | ||
| Ob1 |
| x2 | ||
P = | ||
| 2 |
| x2 | ||
1 = | ||
| x(2+√2) |
| x | ||
1 = | ||
| 2+√2 |
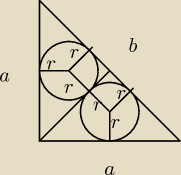 Czy można by to obliczyć zakładając, że b=a+2r a potem podstawiając za a wzór wyprowadzony z
wzoru na przekątną w kwadracie? Zauważyłam, że przy przeciwprostokątnej znajdują się 2
deltoidy o dłuższym boku a/2 czyli w sumie wychodzi z tego a i zostaje jeszcze 2 r. Wydawało
mi się, że można to tak obliczyć, ale nie wychodzi.
Czy można by to obliczyć zakładając, że b=a+2r a potem podstawiając za a wzór wyprowadzony z
wzoru na przekątną w kwadracie? Zauważyłam, że przy przeciwprostokątnej znajdują się 2
deltoidy o dłuższym boku a/2 czyli w sumie wychodzi z tego a i zostaje jeszcze 2 r. Wydawało
mi się, że można to tak obliczyć, ale nie wychodzi.
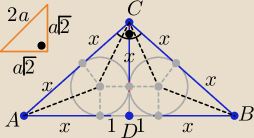 Przy okazji podam takie rozwiazanie:
Obwód ABC =L=6x+2
w trójkącie ADC o kątach 90o,45o,45o
|CD|=x+1 i |CD|= x√2
Przy okazji podam takie rozwiazanie:
Obwód ABC =L=6x+2
w trójkącie ADC o kątach 90o,45o,45o
|CD|=x+1 i |CD|= x√2
| 1 | ||
to: x√2=x+1 ⇒ x√2−x=1 ⇒ x= | = √2+1 | |
| √2−1 |