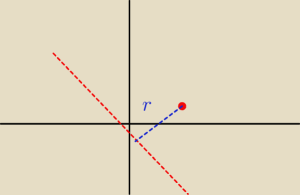
wykaż iiiiiiiiii: kombinuję już z 20 min i nic cały czas WRONG# oto zadanie: wykaż, że prosta l y=−2x−1 jest styczna do okręgu (x−3)²+(y+2)²=5 m.in doszedłem do tego że mamy punkt (3;−2) oraz r= √5 no i nawet narysowałem sobie to w układzie może ktoś to inaczej udowodnić

Krzysiek: znajdz odległosc punktu od prostej i porównaj z promieniem

Saizou : a może algebraicznie

⎧	y=−2x−1
⎩	(x−3)2+(y+2)2=5

jak wychodzi jedno rozwiązanie to znaczy że prosta jest styczna

Aga1.: Odległość punktu S(3,−2) od prostej 2x+y+1=0 musi być równa promieniowi. Lub układ równań prosta+okrąg ma jedno rozwiązanie.

Eta: S(3,−2) r= √5 prosta l: 2x+y+1=0 Aby prosta była styczna do okręgu to odległość d punktu S od tej prostej musi być równa d=r= √5

	3*2−2*1+1|		|5|		5√5
d=		=		=		= √5= r
	√22+12		√5		5

wniosek prosta l jest styczna do tego okręgu

Eta: https://matematykaszkolna.pl/strona/1249.html

iiiiiiiiii: dziękuję wszystkim bardzo mi pomogliście