nierownosc maturzystka: rozwiąż nierównosc Ix² − xI − Ix−5I ≤3 proszę o pomoc, nie wiem jak postępować kiedy pod I I jest f. kwadratowa

maturzystka: kto pomoże ?

ZKS: Dla x ∊ (0 ; 1) −x² + x + x − 5 ≤ 3 x² −2x + 8 ≥ 0 Δ < 0 ⇒ x ∊ R czyli x ∊ (0 ; 1) dla x ∊ (−∞ ; 0> ∪ <1 ; 5) x² − x + x − 5 ≤ 3 x² ≤ 8 ⇒ x ∊ <−2√2 ; 2√2> czyli x ∊ <−2√2 ; 0> ∪ <1 ; 2√2> dla x ∊ <5 ; ∞) x² − x − x − 5 ≤ 3 x² − 2x − 8 ≤ 0 (x + 2)(x − 4) ≤ 0 ⇒ x ∊ <−2 ; 4> Brak rozwiązań. Ostatecznie bierzemy sumę rozwiązań więc x ∊ <−2√2 ; 2√2>.

maturzystka: bardzo dziękuję

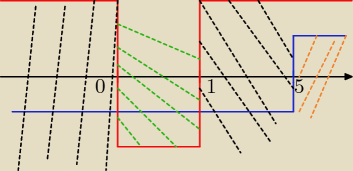
ZKS: Tam gdzie jest zielona lina przerywana obie funkcje przyjmują wartości ujemne x² − x < 0 oraz x − 5 < 0. Czarna linia przerywana funkcja x² − x ≥ 0 ale funkcja x − 5 < 0. Pomarańczowa linia przerywana obie funkcje przyjmują wartości nieujemne x² − x ≥ 0 oraz x − 5 ≥ 0.

maturzystka: wielkie dzięki, już zrozumiałam jak postępować z takimi przypadkami typu I x² − xI Jesteś wspaniały, dziękuję ! Wesołych świąt!

ZKS: Na zdrowie. Wesołych Świąt również życzę.