 Mam zadanko, w którym zdecydowanie utknęłam.
Dla jakich wartości parametru a rozwiązaniem układu nierówności
{ (x−a+7)(x−a)≤0
{ x≤3
Jest przedział długości 4? Odpowiedź uzasadnij.
Więc, wychodzi nam tu ślicznie, ładnie, że
x1=a
x2=a−7
i przedział ten miałby normalnie dł. 7, z tego wynika, że a−7 i a leżą po obu stronach 3−jki.
nie wiemy, czy a−7, czy a jest większe, ale mamy założenie, że x≤3⇒ a≤3
i teraz chciałam policzyć tę a z dł. przedziału, więc
|a−3|= 4 lub |a−7−3|=4
a=7 (sprz) a=−1 (
Mam zadanko, w którym zdecydowanie utknęłam.
Dla jakich wartości parametru a rozwiązaniem układu nierówności
{ (x−a+7)(x−a)≤0
{ x≤3
Jest przedział długości 4? Odpowiedź uzasadnij.
Więc, wychodzi nam tu ślicznie, ładnie, że
x1=a
x2=a−7
i przedział ten miałby normalnie dł. 7, z tego wynika, że a−7 i a leżą po obu stronach 3−jki.
nie wiemy, czy a−7, czy a jest większe, ale mamy założenie, że x≤3⇒ a≤3
i teraz chciałam policzyć tę a z dł. przedziału, więc
|a−3|= 4 lub |a−7−3|=4
a=7 (sprz) a=−1 ( ) a=14 (sprz) lub a=6
) a=14 (sprz) lub a=6  odp. to właśnie 6, nie mam pojęcia, dlaczego wychodzi tam też to −1
odp. to właśnie 6, nie mam pojęcia, dlaczego wychodzi tam też to −1 
 Odległość a − 7 do 3 mus być równa 4, i WIEMY, że a − 7 jest mniejsze od a !
Odległość a − 7 do 3 mus być równa 4, i WIEMY, że a − 7 jest mniejsze od a !  Pozostaje rozwiązać:
|a − 7 − 3| = 4
|a − 10| = 4
a − 10 = 4 lub a − 10 = −4
a = 14 lub a = 6, dlaczego 14 nie pasuje ? Ano dlatego, że pracuje nam założenie, że x ≤ 3.
Odp: a = 6
Pozostaje rozwiązać:
|a − 7 − 3| = 4
|a − 10| = 4
a − 10 = 4 lub a − 10 = −4
a = 14 lub a = 6, dlaczego 14 nie pasuje ? Ano dlatego, że pracuje nam założenie, że x ≤ 3.
Odp: a = 6
 Mądra nie zauważyłam, że nieważne, czy a jest dodatnie, czy ujemne,
a−7 zawsze będzie mniejsze.
Mądra nie zauważyłam, że nieważne, czy a jest dodatnie, czy ujemne,
a−7 zawsze będzie mniejsze.  Niech Ci Bozia w dzieciach wynagrodzi, Godzio
Niech Ci Bozia w dzieciach wynagrodzi, Godzio 



 Udowodnij, że dla dowolnych a,b∊R prawdziwa jest nierówność
5a2+4a−2ab+b2+2>0
tu szybciutko: (2a+1)2+(a−b)2>0 no i .... tam nie powinno być ≥0? zamiast >0? Przecież oba
nawiasy mogą być równe 0... chyba
Udowodnij, że dla dowolnych a,b∊R prawdziwa jest nierówność
5a2+4a−2ab+b2+2>0
tu szybciutko: (2a+1)2+(a−b)2>0 no i .... tam nie powinno być ≥0? zamiast >0? Przecież oba
nawiasy mogą być równe 0... chyba 
 . ...
. ... 
 Dzięki Pigor
Dzięki Pigor 
 , a nawet , więcej to pierwsze nigdy nie będzie zero ...
, a nawet , więcej to pierwsze nigdy nie będzie zero ... 
| 1 | ||
A dlaczego? dla a=− | ...? | |
| 2 |
| 1 | ||
a = − | ||
| 2 |
| 1 | ||
b = − | i mamy problem  | |
| 2 |
 Wiedziałam, że widzę tu gdzieś sprzeczność
Wiedziałam, że widzę tu gdzieś sprzeczność 

 faktycznie , to może ktoś zamiast ≥ ...
faktycznie , to może ktoś zamiast ≥ ... 
 to teraz...
to teraz...  jasne
jasne
 Basiu każdy się myli. Jakub przewidział taką sytuację i pewnie specjalnie nie dodał
takich emotikon
Basiu każdy się myli. Jakub przewidział taką sytuację i pewnie specjalnie nie dodał
takich emotikon 
 urwany
urwany 
 Wrócę wieczorkiem, bo już widzę kolejne problemy
Wrócę wieczorkiem, bo już widzę kolejne problemy 
 Nie wiem, co ze mną jest nie tak, ale coś na pewno
Nie wiem, co ze mną jest nie tak, ale coś na pewno 



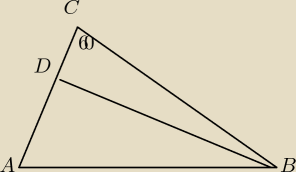 Zadanko:
w trójkącie ABC dane są ∡ACB=60 i AB=√31. Na boku AC obrano taki punkt D, że dł. odcinka AD
wynosi 3. Znajdź długość boku BC, jeśli |BD|=2√7.
Kombinuję, kombinuję i wychodzą mi... głupoty.
Zadanko:
w trójkącie ABC dane są ∡ACB=60 i AB=√31. Na boku AC obrano taki punkt D, że dł. odcinka AD
wynosi 3. Znajdź długość boku BC, jeśli |BD|=2√7.
Kombinuję, kombinuję i wychodzą mi... głupoty. 



| 2 | ||
cosα = | ||
| √31 |
| 2√31 | ||
cosα = | ||
| 31 |
 sin2α + cos2α = 1 ...
3o Zastosować tw. sinusów:
Oznaczę sobie |BC| = x, i jedziemy:
sin2α + cos2α = 1 ...
3o Zastosować tw. sinusów:
Oznaczę sobie |BC| = x, i jedziemy:
| x | √31 | ||
= | |||
| sinα | sin60o |
 Tak na szybko, nawet nie zdążyłem się rozebrać po powrocie z Kościoła
Tak na szybko, nawet nie zdążyłem się rozebrać po powrocie z Kościoła 
 Postaram się rozgryźć sama.
Postaram się rozgryźć sama.





 Ja się do takich rzeczy nie zbliżam.
Ja się do takich rzeczy nie zbliżam. 