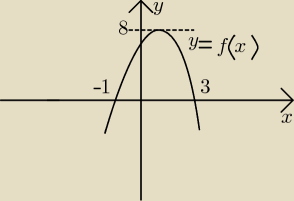
Na rysunku obok Danio: Na rysunku obok przedstawiony jest wykres funkcji kwadratowej f(x)= m(x−a)²+b, gdzie m<0. Wykresfunkcji f przecina oś OX w punktach o wspolrzednych (−1,0) oraz (3,0), zaś punkt W(a,8) jest wierzchołkiem tej paraboli. Wyznacz a,b oraz m.

vladimirovna: Ja zrobiłabym to tak: f(−1)=0 f(3)=0 0=m(−1−a)²+b 0=m(3−a)²+b f(x)=mx²+ma²−2max+b f(x)=mx²−2max+ma²+b ^−Δ_4m=8 ale nie wiem, czy cos z tego wyjdzie, bo tego nie liczylam

vladimirovna: wyszło mi tak: b= −8, m=8 i a=2

Skipper: czy napewno a=2 ? −

vladimirovna: tak, tak mi wyszło, ale ja nie ręczę za moje rozwiązanie, bo często mi się zdarza robić pomyłki

Skipper: skoro W=(a,8) x₁=−1 x₂=3 ...to a=1

Danio: 0=m(−1−a)2+b 0=m(3−a)2+b Ja to dalej policzyłem: 0=m+2am+ma²+b /x(−1) 0=9m−6am+ma²+b i wyszlo mi z tego coś takiego : 0=8m−8am. Potem am=m i a=m/m. Czy to juz wystarczy by wyszlo a=1 i m=8? Bo z tego to juz widze ale nie wiem czy na maturze to byloby uznane.

Paula: fajnie ze wychodzi wam m=8 skoro ma byc mniejsze od 0. ja liczylam i wychodzi b=8 a=1 a m=−2 dziekuje

Mila: Jeśli masz podane miejsca zerowe, to

	x1+x2
xw=		⇔ (prosta x=xw jest osią symetrii paraboli)
	2

	−1+3
xw=		=1 i z rysunku wiadomo, że f(1)=8
	2

Postać kanoniczna f(x)=m(x−1)²+8 f(3)=0⇔m(3−1)²+8=0⇔m*4=−8 m=−2 f(x)=−2(x−1)²+8