Proszę o pomoc w tym zadaniu
Majutka:
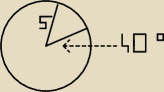
Koło o promieniu długości 5 rozcięto na dwa wycinki. Jeden z wycinków odpowiada kątowi
środkowemu o mierze 40
o. Z każdego wycinka utworzono powierzchnię boczną stożka. Oblicz
sumę długości promieni podstaw tych stożków.
16 kwi 15:20
Majutka: Bardzo proszę xpt o pomoc w tym zadaniu

16 kwi 15:38
16 kwi 15:48
Majutka: Czyli z tego wzoru l= α
___ *2πr
360o
16 kwi 15:56
Majutka: 
16 kwi 15:56
tim: Tak, tylko zamiast l pisz Ob ub Obwód

16 kwi 15:59
Majutka: dobrze

ale chyba mi coś źle wyszło bo mam 10/9π ?
i co dalej ?
16 kwi 16:07
tim: | 10 | |
| π, jest dobry  |
| 9 | |
Więc znasz obwód podstawy stożka, więc
| | 10 | |
2πR, gdzie R = promień stożka = |
| π |
| | 9 | |
Podstaw i oblicz R.
16 kwi 16:08
Majutka: nie zbyt rozumiem jak to zapisać ?
2πR = 2π * 10/9π =...?
16 kwi 16:14
tim: oj, źle zapisałem
| | 10 | |
2πR = |
| π, gdzie R = promień stożka  |
| | 9 | |
16 kwi 16:15
Majutka: 10
2πR =___ |*9
9
18R=10 |:18
R=10/18= 5/9
coś chyba nie takk ?
16 kwi 16:20
tim: Czemu?

Teraz policz ile można utworzyć stożków z koła
16 kwi 16:29
tim: Teoretycznie jest drugie rozwiązanie. Na logikę. Skoro z całego koła o r = 5 utworzono 9
stożków, to suma P
b stożków równa się polu koła, więc 2πr = 2πR, więc S
R = 5

16 kwi 16:32
Majutka: a jak to obliczyć żeby mi wyszło ile można zrobić stożków ? Bo nie mam pojecia

16 kwi 16:51
tim: Jeden stożek zajmuje 40/360 koła. Ile to?
16 kwi 16:53
Majutka: o.O 1/9 ?
16 kwi 16:56
tim: Tak. Czyli ile można?
16 kwi 16:56
Majutka: A możesz mi wytłumaczyć skąd się wzieło to 40/360 ?
16 kwi 16:59
tim: Bo kąt ma 40O?
16 kwi 17:03
Majutka: aHa
Więc ile można ich zrobić ? Bo nie wiem ?
16 kwi 17:23
tim: Skoro jeden zajmuje 1/9 to ile zajmie 1 całe?
16 kwi 17:25
Majutka: nie mam pojecia

16 kwi 17:29
tim: No 9*

16 kwi 17:31
Majutka: To coś chyba wyszło nie takk. Bo w książce w oDp. mam ,że ma wyjść 5

uPs.
16 kwi 17:34
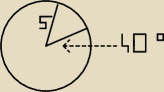 Koło o promieniu długości 5 rozcięto na dwa wycinki. Jeden z wycinków odpowiada kątowi
środkowemu o mierze 40o. Z każdego wycinka utworzono powierzchnię boczną stożka. Oblicz
sumę długości promieni podstaw tych stożków.
Koło o promieniu długości 5 rozcięto na dwa wycinki. Jeden z wycinków odpowiada kątowi
środkowemu o mierze 40o. Z każdego wycinka utworzono powierzchnię boczną stożka. Oblicz
sumę długości promieni podstaw tych stożków.



 ale chyba mi coś źle wyszło bo mam 10/9π ?
i co dalej ?
ale chyba mi coś źle wyszło bo mam 10/9π ?
i co dalej ?


 Teraz policz ile można utworzyć stożków z koła
Teraz policz ile można utworzyć stożków z koła




 uPs.
uPs.