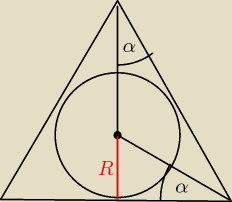
α=30o
R − promień kuli
r − promień stożka
H − wysokość stożka
Przekrój osiowy stożka jest trójkątem równobocznym, z czego wynika, że H=3R, można też to sobie
z trójkątów 30,60,90 policzyć jakby ktoś nie wierzył.
r=R√3
VΔ = 13π * 3R * R = 3R3π
VO = 43πR3
VΔVO = 32
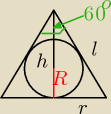Skoro kąt przy wierzchołku ma 60o, to ten trójkąt jest [P{równoboczny]], czyli:
l = 2r
| 2r√3 | ||
i h = | = r√3
| |
| 2 |
| 1 | 1 | √3πr3 | ||||
Vs = | πr2h = | πr2*r√3 = | ||||
| 3 | 3 | 3 |
| 1 | √3 | |||
R − promień kuli: R = | h = | r
| ||
| 3 | 3 |
| 4 | 4 | √3 | 4√3πr3 | |||||
Vk = | πR3 = | π* | r3 = | |||||
| 3 | 3 | 9 | 27 |
| Vs | √3πr3 | 27 | 9 | ||||
= | * | = | |||||
| Vk | 3 | 4√3πr3 | 4 |
promień podstawy stożka a/2
| a√3 | ||
wysokość stożka | ||
| 2 |
| πa3√3 | ||||||||||||
Vs= | = | ||||||||||||
| 3 | 24 |
| a√3 | ||
Promień kuli | ||
| 6 |
| 4π | 3√3a3 | πa3√3 | ||||
Vk= | * | = | ||||
| 3 | 63 | 54 |
| Vs | 9 | ||
= | |||
| Vk | 4 |
