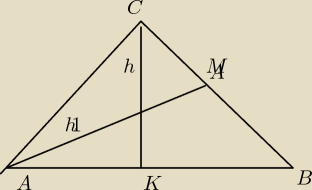
Planimetria Krl: W trójkącie równoramiennym ABC poprowadzono wysokości AM i CK. Wiedząc że AB²=AM*CK wyznacz cosinus kąta przy podstawie trójkąta. Moje rozwiązanie: AB=a a²=h*h₁ Z porównania pól ABC: b*h₁=ah

	ah
b=
	h1

	a		h1
cosα=		=
	2b		2h

	h1		h12
W ΔABM: sinα=		⇔ cosα=1−sin2α= 1−		⇔ (podstawiam pod a założenie z
	a		a2

	h12		h−h1
zadania) 1−		=
	h*h1		h

Teraz porównuje cosinusy:

h1		h−h1		2h
	=		⇔ h1=
2h		h		3

	1
cosα=
	3

Odp prawidłowa: √2−1

Beti: I czego oczekujesz? sprawdzenia? Jeśli tak, to znalazłam błąd − obliczenia w trójkącie ABM: napisałeś, że cosα = 1−sin²α. Powinno być: cos²α = 1−sin²α.

Krl: Rzeczywiście, ale jak dalej iść z czymś takim. Da sie tym spsobem dojść do wyniku prawidłowego czy od nowa innym?

Beti: Ja zrobiłam inaczej w drugiej części, czyli zamiast ΔABM wykorzystałam tw. Pitagorasa dla ΔKBC. Wyszło √2−1, czyli metoda skuteczna

pigor: ... ja bym "robił" to np. tak : niech cosα=? , gdzie α − wspólna miara ostrych kątów : ∡ABM i ∡KBC prostokątnych : ΔAMB i ΔBKC odpowiednio, to z warunków zadania : AB² = AM*CK / : AB² ⇔ 1= ^AM_AB* ^CK_AB ⇔ 1= sinα * ^CK_2KB /*2 ⇔ 2 = sinα*tgα / *cosα ⇒ 2cosα = sin²α ⇔ 2cosα = 1−cos²α ⇔ cos²α+2cosα−1=0 ⇔ ⇔ cos²α+2cosα+1−2=0 ⇔ (cosα+1)²=2 ⇔ |cosα+1|=√2 ⇒ cosα+1=√2 ⇔ ⇔ cosα=√2−1 − szukana wartość cosinusa . ...