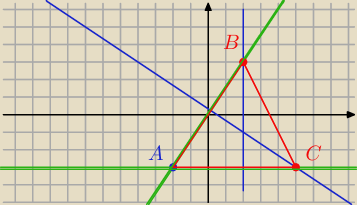
Dwie wysokości i wierzch A . Oblicz wsp. pozostałych wierzchołków BigMax: Dwie wysokości trójkąta ABC, gdzie A = (−2,−3), zawarte są w prostych o równaniach x − 2 = 0 i 2x+3y−1=0. Oblicz współrzędne pozostałych wierzchołków tego trójkąta.

Basia: Rozwiązuję

Basia: k: x − 2 = 0 x = 2 A nie należy do k bo −2≠2 k || OY l: 2x + 3y − 1 = 0 2*(−2) + 3*(−3) − 1 = −4 − 9 − 1 = −14 ≠0 A nie należy do l wynika stąd, że k = BB₁ i l=CC₁ (lub na odwrót, ale to nie ma znaczenia) BB₁ jest prostopadła do pr.AC pr.AC || OX pr.AC: y = b −3 = b y = −3 B ∈pr.BB₁ ⇒ B(2,y) C∈pr.AC ⇒ C(x,−3) C∈pr. CC₁ 2x + 3*(−3) − 1 = 0 2x −10=0 2x=10 x=5 C(5,−3) CC₁ jest prostopadła do pr.AB 2x − 3y − 1 = 0 2x − 1 = 3y

	2		1
y =		x −
	3		3

	3
pr.AB: y =−		x + d
	2

A∈ pr.AB

	3
−3 = −		*(−2) + d
	2

−3 = 3 + d d = −6

	3
pr.AB: y = −		x − 6
	2

2y = −3x − 12 3x + 2y = −12 B ∈pr.AB B(2,y) 3*2 + 2y = −12 6 + 2y = −12 2y = −18 y = −9 B(2;−9)

Crax:

	2
2x+3y−1=0 ⇒ a = −
	3

	3
prosta równoległa a1 =
	2

	3
A ∊ y =		x +b
	2

	3
A(−2,−3) ⇒ y =		x
	2

	3
B ∊ y =		x
	2

B(2,y) ⇒ y = 3 B(2,3)

Qulka: