. DSGN.: Punkty A(5, 6) i B(−1, 3) są końcami jednej z wysokości trójkąta równobocznego. Napisz równanie okręgu opisanego na trójkącie oraz wpisanego w ten trójkąt, wiedząc że punkt B nie jest jego wierzchołkiem. Bo coś mi z moich obiczen nie idzie poproszę liste kroków

Eta: Zaraz Godzio "wkroczy" ( bo podobno się nudzi?

DSGN.: no to czekamy chyba ze juz spi

Eta: S(1,4) r= √5 R=2√5 równanie okręgu wpisanego o: (x−1)²+(y−4)²=5 opisanego o: (x−1)²+(y−4)²= 20

Godzio: Hmmm

DSGN.: dzięki choć prosiłem o listę kroków, ale jak to sie mówi:" darowanemu koniowi nie zagląda się w zęby"

Eta:

	2		1
R=		|AB| r=		|AB|
	3		3

→ →

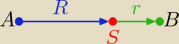
	2
S(x,y) AS =		AB wyznacz współrzędne S
	3

Eta:

Godzio: A(5,6) B(−1,3) 6 = 5a + b 3 = −a + b 3 = 6a

	1		7
a =		⇒ b =
	2		2

	1		7
y =		x +		⇒ x − 2y + 7 =0
	2		2

Odległość B od środka jest długością promienia okręgu wpisanego w ten trójkąt, dajmy, że środek to S(2b − 7,b) (bo należy do naszej prostej)

	1		1		1
r =		h =		|AB| =		* √36 + 9 = √5
	3		3		3

|BS| = √5 /² (−1 − 2b + 7)² + (3 − b)² = 5 ⇒ 4b² − 24b + 36 + 9 − 6b + b² = 5 5b² − 30b + 40 = 0 b² − 6b + 8 = 0 (b − 4)(b − 2) = 0 b = 4 lub b = 2 S(1,4) lub S(−3,2), i teraz jedno wywalasz (już po odpowiedzi wiesz które) teraz do Ciebie pytanie dlaczego ?

Godzio: Łojej, ale żem o Paryż zahaczył

Eta:

DSGN.: możesz sie łatwo zrehabilitować wykazując ze dla dowolnego całkowitego m liczba

	1
		*[3m(m+3)(2m2+6m+4)+6] jest kwadratem liczby całkowitej w sumie to prosty wykaz
	6

Godzio: m(m + 3)(m² + 3m + 2) + 1 = m(m + 1)(m + 2)(m + 3) + 1 = m⁴ + 6m³ + 11m² + 6m + 1 = m⁴ + 9m² + 1 + 6m³ + 2m² + 6m = (m² + 3m + 1)²

DSGN.: a tu 2 sposobik

	1		1		1
=		[6(m2+3m+1−1)(m2+3m+1+1)+6]=		{6[(m2+3m+1)2−12]+6}=
	6		6		6

[6(m²+3m+1)²−6+6]=(m²+3m+1)²