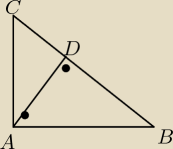
planimetria blogther: W trojkacie prostokatnym stosunek przyprostokatnych jest rowny ⁷₂. Wykaz ze wysokosc poprowadzona z wierzcholka kata prostego dzieli przeciwprostokatna na dwa odcinki ktorych stosunek jest rowny ⁴⁹₄. AC=7x AB=2x z twierdzenia Pitagorasa BC= x√53

	14x√53
AD wyznaczam porownojac wzory na pole trojkata i wyznaczam ze AD=
	53

z twierdzenia Pitagorasa w ΔABD BD² = AB² + AD²

	2x√102
BD =
	√53

z twierdzenia Pitagorasa w ΔACD DC²= AD² + AC²

	7x√102
DC=
	√53

	DC		7
i teraz		=
	BD		2

a my wykazac ze ten stosunek wynosi ⁴⁹₄ gdzie mam bład?

Mila: Błędnie zapisane tw Pitagorasa AB²=AD²+BD² AC²=...

blogther: okey dzieki juz widze

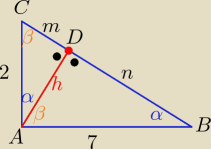Eta: m,n>0

	m		h
ΔABD ~ΔADC ⇒		=		⇒ h2= m*n , h>0
	h		n

to h= √m*n oraz

	m		h
sinα=		=		⇒ 7m= 2√mn /2
	2		7

49m²= 4mn / :m 49m= 4n

	n		49
		=
	m		4