wektory piotrek123: Witajcie, mam problem z paroma zadaniami. Mógłby ktoś pomóc? 1. Wykaż, że jeśli punkty R,M,N są środkami odpowiednio boków BC, CA, AB trójkąta ABC to długość wektora AB+ dł.wekt. BM+ dł. wekt. CN = 0 2. Punkty A=(1,2), B=(−1,−1), C=(5,2) są wierzchołkami trójkąta a) napisz równanie prostej zawierającej wysokość tego trójkąta poprowadzoną z wierzchołka A oraz napisz współrzędne spodka wysokości b) wyznacz współrzędne punktu D, aby czworokąt ABCD był równległobokiem 3. W okrąg o promieniu długości 7 wpisano czworokąt ABCD. Oblicz obwód i pole czworokąta wiedząc, że IABI=IBCI, a kąt ADC=120 stopni i stosunek trójkąta ABD do pola trójkąta BCD jest równy 2:1.

Basia: ad.1 niemożliwe; długości to liczby dodatnie; suma liczb dodatnich na pewno nie jest równa 0 coś musiałeś źle przepisać

piotrek123: oczywiście, to nie mają być długości tylko po prostu wektory

piotrek123: ponawiam prośbę o pomoc bo nijak sobie nie daję rady

Basia: Dochodzę do sprzeczności Eto (w 3), ale jeszcze sprawdzę.

Basia: A nie, pomyliłam się

Basia: Mam rozwiązanie (3). Pisać ?

Eta: W 3/ wyszły mi nieco koszmarniane wyniki, i nie wiem czy się gdzieś nie pomyliłam?

Eta: Napisz tylko wynik

Eta: Mnie wyszło : Ob= 3√21 +14√3 a pole: P= ^189p{3₄

Eta: Oczywiście : P=^189√3₄

Basia: Inny mam, ale mogłam się pomylić. Policzę jeszcze raz.

Eta: A może ja się pomyliłam ?

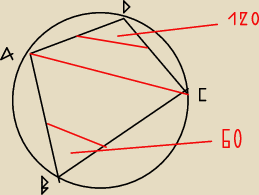
Basia: AB = BC = x ⇒ AC=x R = 7

	2
R =		h
	3

	2
7 =		h
	3

	21
h =
	2

	x√3
h =
	2

21		x√3
	=
2		2

x√3 = 21

	21√3
x =
	3

x = 7√3

	49*3*√3		147√3
P1 =		=
	4		4

AB=BC=y

	y*AD*sinα
PABD =
	2

	y*CD*sin(180−α)
PBCD =
	2

y*AD*sinα
	= 2
y*CD*sinα

AD
	= 2
CD

AD = 2CD x² = y² + 4y² − 4y²*cos120 x² = 5y² + 2y² = 7y² x² = 7y² (7√3)² = 7y² 7*7*3 = 7y² y² = 21 y = √21

	y*2y*sin120		21√3
P2=		= y2*sin120 =
	2		2

	189√3
P =
	4

Ob = 14√3 + 3√21 = √3(14+3√7) tak samo wyszło; przedtem się pomyliłam

Eta: Dzięki Ok Tak samo liczyłam Myślałam ,że się pomyliłam w r−ach PS: Nie ma co robić?.... zagram chyba w brydża ?

Basia: ad1. to ma być: (nie piszę strzałek, cały czas wektory) AR + BM + CN

	1
AR = AB + BR = AB +		BC
	2

	1
BM = BA + AM = −AB +		AC
	2

	1		1
CN = CA + AN = AC +		AB = − AC +		AB
	2		2

	1		1
CN = CB + BN = −BC +		BA = − BC −		AB
	2		2

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	1		1
2CN = −AC +		AB − BC −		AB
	2		2

	1		1
CN = −		AC −		BC
	2		2

	1		1		1		1
AR + BM + CN = AB +		BC − AB +		AC −		AC −		BC =0
	2		2		2		2

Basia: 2. Punkty A=(1,2), B=(−1,−1), C=(5,2) są wierzchołkami trójkąta a) napisz równanie prostej zawierającej wysokość tego trójkąta poprowadzoną z wierzchołka A oraz napisz współrzędne spodka wysokości b) wyznacz współrzędne punktu D, aby czworokąt ABCD był równległobokiem wysokość AA₁ jest prostopadła do BC napisz równanie prostej BC przekształć go do postaci y = ax + b

	1
pr.AA1 ma równanie y = −		x + c
	a

c wyznacz na podstawie tego, że A∈pr.AA₁ spodek wysokości A₁ to punkt wspólny pr. BC i pr.AA₁ rozwiązujesz układ równań ad.b w równoległoboku → → AB = DC a równe wektory mają takie same współrzędne

piotrek123: dzięki