Zadanie z podobienstwa "suma kombinacji" Kondzio: Z grupy osób, w której jest 5 kobiet , wybrano 3 osobową delegacje. Prawdopodobieństwo tego, że w delegacji jest więcej kobiet niż mężczyzn wynosi 6/7. Oblicz ilu jest mężczyzn w tej grupie. z tego co zrozumiałem z zadania to że trzeba rozwiązywać zadanie z kombinacji bo nie jest ważna kolejność. |Ω|= (5+n)(4+n)(3+n) ale problem mam z A gdyż ... muszą być 2 kobiety a ostatni musi być wylosowany z całej grupy ... czyżby więc

	n+5 1		5 2
|A|=		[i tu ma być * ?] *

i z tego mi wyszło coś takiego : n³ + 4*n² + 31*n +5 =0 i jak to niby rozwiązać?!

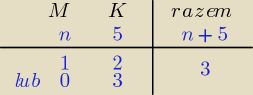
Artur z miasta Neptuna: po pierwsze .... nie do końca dobrze rozumujesz, bo: jest więcej kobiet niż mężczyzn oznacza, że delegacja jest postaci: 2k i 1m LUB 3k

	5 2		n 1		5 3
|A| =		*		+

bo wybierasz z danej grupy ileś osób

Artur z miasta Neptuna: Ω też masz źle wyznaczoną ... |Ω| ≠ (5+n)(4+n)(3+n) jeżeli zakładasz, że kolejność nie gra roli (w takiej Ω kolejność odgrywa rolę) więc albo zmieniasz |Ω| albo |A|, którą podałem wyżej

Bogdan:

	n + 5 3		(n + 5)(n + 4)(n + 3)
|Ω| =		=
			1*2*3

n 1

5 2

n 0

5 3

5*4

5*4*3

|A| =

*

+

*

= n*

+ 1*

= 10(n + 1)

1*2

1*2*3

	10(n + 1)		6
P(A) =		=
	(n + 5)(n + 4)(n + 3)     1*2*3		7

Po uporządkowaniu otrzymujemy równanie: n³ + 12n² − 23n − 10 = 0 i n∊N₊ Równanie to jest spełnione dla n = 2