Oblicz objętość stożka. Sylwia: 1 Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 12. Oblicz objętość tego stożka. 2 Tworząca stożka ma 18 cm i jest nachylona do płaszczyzny podstawy pod kątem 45◯. Oblicz pole powierzchni bocznej stożka 3 0blicz objętość walca, jeśli jego wysokość ma 8cm, a przekątna przekroju osiowego ma 17 cm. 4. W ostrosłupie prawidłowym sześciokątnym o wysokości h=2√3 krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60◯(stopni) Oblicz objętość tego ostrosłupa.

Domiś: zad 1. wysokość stożka to wysokość przekroju czyli : h=a√3/2 h=12√3/2 h=6{3} promień podstawy stożka to połowa boku przekroju czyli 12/2=6 teraz obliczamy objętość ze wzoru : V=1/3*π*r²*h po podstawieniu wychodzi że V=72√3π

Sylwia: a udało by Ci się rozwiązać resztę zdań ?

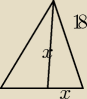
Domiś: zad.2 Znając kąt nachylenia (45stopni) możemy skorzystać z własności przekątnych kwadratu. W tym przypadku tworząca stożka jest przekątną kwadratu czyli 18=a√2 czyli a=r=9√2 teraz zw wzoru na pow.boczn.stoż.=π*r*l=π*9√2*18 = 162√2π

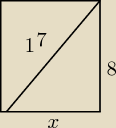
Domiś: zad.3 Z twierdzenia pitagorasa liczysz średnicę podstawy walca x² * 8² = 17² x=15 promień podstawy to połowa x czyli 7,5 i wzór na objętość : V=Pp*H V=πr² * 8 V=56.25*8*π V=450π

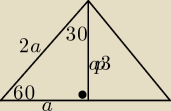
Domiś: zad.4 z własności trójkąta o kątach 30, 90, 60 : (narysuję ci przekrój osiowy ostrosłupa) 1−wysokość to 2√3 czyli bok a ma miarę 2 w podstawie mamy sześć trójkątów równobocznych czyli krawędź podstawy również ma miarę 2. ze wzoru na pole sześciokąta foremnego liczymy pole podstawy: P=3a^a√3/2 jak podstawisz wyjdzie Ci że P=6√3 i liczysz objętość V= Pp*h V=6√3 * 2√3 v=36

Sylwia: rozwiązała byś mi jeszcze 2 zadania?