ciągi geometryczne
marek: W kwadrat o danym boku 1 wpisujemy drugi kwadrat w ten sposób , że jego wierzchołki są środkami
boków danego kwadratu. W drugi kwadrat wpisujemy trzeci kwadrat w ten sam sposób co drugi i
tak dalej. wykaż , że ciąg pól kolejnych kwadratów jest ciągiem geometrycznym
2 kwi 19:58
Skipper:
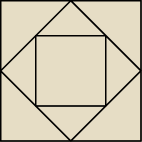
| | a | | a | |
boki są odpowiednio ... a, |
| , |
|
|
| | √2 | | √2√2 | |
| | 1 | |
stanowią ciąg arytmetyczny b1=a q= |
|
|
| | √2 | |
zatem pola stanowią też ciąg geometryczn taki, że
c
1=a
2 q=1/2
2 kwi 20:41
marek: a mozesz wytłumaczyc to co napisałes na pod obrazkiem?
2 kwi 20:59
marek: Skipper prosze...
2 kwi 21:09
Skipper:
nie zauważyłem że bok pierwszego równy jest 1 (a nie a ... jak ja założyłem)
2 kwi 21:15
Skipper: bok największego kwadratu ... 1
| | 1 | |
bok kolejnego √(1/2)2+(1/2)2= |
| ... itd |
| | √2 | |
2 kwi 21:19
marek: te długości boków rozumiem... ale jak to dokładnie udowodnic, ze to ciag geometryczny?
2 kwi 21:24
Pat: moim zdaniem mozesz po prostu policzyc 3 pierwsze pola, czyli
P1=1, P2=2/4, P3=4/16 (zeby obliczyc pola liczysz poszczegolne boki kwadratow z tw.
Pitagorasa)
i udowodnic, ze jak dzielisz P2/P1 i P3/P4 wychodzi takie same q, wiec ciag jest geometryczny
q wychodzi 2/4
2 kwi 21:52
Skipper: | | √2 | |
nie widzisz, że boki stanowią ciąg a1=1 q= |
|
|
| | 2 | |
kolejny bok jest przekątną kwadratu na połówkach poprzedniego boku
2 kwi 21:55
