 Wykres powyżej obrazowy
Wykres powyżej obrazowy  Dana jest funkcja f(x)=|(x−m)2−4m|, gdzie m € R:
a) Naszkicuj wykres funkcji f(x) dla m=1.
b) Dla jakich wartości parametru m równanie f(x)=7 ma dokładnie trzy rozwiązania.
Zabrałem się do tego, ale prawdopodobnie źle, więc proszę o skorygowanie błędów i ew.
pomoc
Dana jest funkcja f(x)=|(x−m)2−4m|, gdzie m € R:
a) Naszkicuj wykres funkcji f(x) dla m=1.
b) Dla jakich wartości parametru m równanie f(x)=7 ma dokładnie trzy rozwiązania.
Zabrałem się do tego, ale prawdopodobnie źle, więc proszę o skorygowanie błędów i ew.
pomoc  :
a) m=1
f(x)=|(x−m)2−4m|
f(x)=|{x−1)2−4*1|
f(x)=(x+1)2+4
f(x)=x2+2x+5
Δ=4−20=−16
Δ<0, a>0
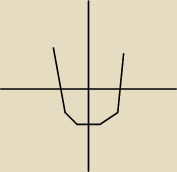
Wykres naszkicowany powyżej (jeśli dobrze rozumiem "naszkicuj" tzn. że mam pokazać
jak są zwrócone ramiona i czy wykres jest pod czy nad osią x, prawda?)
:
a) m=1
f(x)=|(x−m)2−4m|
f(x)=|{x−1)2−4*1|
f(x)=(x+1)2+4
f(x)=x2+2x+5
Δ=4−20=−16
Δ<0, a>0
Wykres naszkicowany powyżej (jeśli dobrze rozumiem "naszkicuj" tzn. że mam pokazać
jak są zwrócone ramiona i czy wykres jest pod czy nad osią x, prawda?) b) f(x)=7 (tutaj się pogubiłem i na pewno źle coś robię)
b) f(x)=7 (tutaj się pogubiłem i na pewno źle coś robię) 7=|(x−m)2−4m|
7=(x+m)2+4m
7=x2+2xm+2m+4m − i tutaj poległem
7=|(x−m)2−4m|
7=(x+m)2+4m
7=x2+2xm+2m+4m − i tutaj poległem 
| 2−4 | ||
x1 = | = −1 | |
| 2 |
| 2+4 | ||
x2 = | = 3 | |
| 2 |
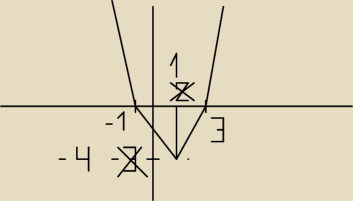 i teraz to co jest "pod osią OX" przekształcasz w symetrii osiowej względem OX
rysunek za chwilę
i teraz to co jest "pod osią OX" przekształcasz w symetrii osiowej względem OX
rysunek za chwilę
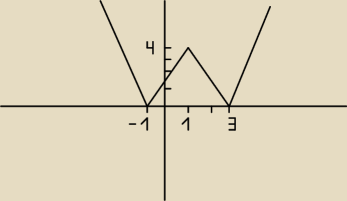 to jest wykres Twojej funkcji, oczywiście to mają być fragmenty paraboli a nie proste,
ale ja tu krzywych rysować nie umiem
to jest wykres Twojej funkcji, oczywiście to mają być fragmenty paraboli a nie proste,
ale ja tu krzywych rysować nie umiem
| 28 | 7 | |||
m ≥ − | = − | |||
| 16 | 4 |
| 28 | 7 | |||
m ≥ | = | |||
| 16 | 4 |
| 7 | ||
gdyby Δ1 = 0 ⇒ m = − | i Δ2 byłaby ujemna czyli źle bo drugie nie miało by | |
| 4 |
| 7 | ||
Δ2 = 0 ⇔ m = | (drugie ma jedno rozw.) | |
| 4 |
| 7 | 7 | ||
> − | ⇒ Δ1> 0 ⇒ pierwsze ma dwa rozw. | ||
| 4 | 4 |


