Błagam o szybką pomoc
Kazio:

| | a+b | |
Trapez równoramienny Udowodnij, że |
| =r |
| | 2 | |
2 kwi 17:07
M:
9 lut 09:49
Pick:
No i Kazio 13 lat temu nie wybłagał
9 lut 13:10
NN:
To teraz "Picuś" pomoże

9 lut 13:14
Goblin:
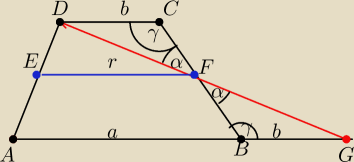
Mamy już udowodnione takie twierdzenie
Twierdzenie :
Odcinek łączący środki dowolnych dwóch boków trójkąta jest równoległy do boku trzeciego i równy
jego połowie.
Mamy do udowodnienia twierdzenie
Twierdzenie:
Linia środkowa trapezu jest równoległa do obu podstaw i równa połowie sumy tych podstaw.
AB=a
CD=b
EF=r
Założenie ;
EF jest linia srodkową trapezu (czyli DE=DA i CF=FB )
Teza:
| | AB+CD | |
EFIIAB i EFII CD oraz EF= |
| |
| | 2 | |
Dowód.
Do dowodu wykreślamy z wierzchołka D przez punkt F prosta która przetnie przedłużenie podstawy
AB w punkcie G.
Rozważmy teraz dwa trójkąty ,ΔDFC i ΔFBG
Trójkąty te są przystające na podstawie cechy (kbk) dlatego że :
CF=FB z założenia
∡DCF=∡FBG jako kąty naprzemianległe wewnętrzne
∡DFC=∡BFG jako kąty wierzchołkowe
Z przystawania tych trójkątów wynika że
CD=BG
Zatem odcinek AG jest równy sumie obu podstaw czyli
AG=AB+BG
Rozpatrzmy teraz ΔADG .
Z udowodnionego wcześniej twierdzenia o linii środkowej trójkąta widzimy że odcinek EF łączy
środki dwóch boków tego trójkąta −wobec czego jest równoległy do boku trzeciego AG (EF II
AG)ii równy połowie tego boku.
Więc udowodniliśmy że EF jest równoległe do AB i też do CD i równe połowie sumy AC+CD
9 lut 13:28
Jasiek:
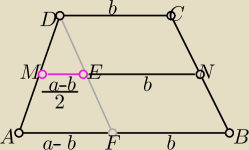
|AF|=a−b
9 lut 13:36
Jasiek:
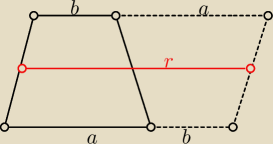
9 lut 13:41
Pick:
Kazio nie podał czym jest odcinek oznaczony literką r, czy jest równoległy do podstaw
i czy łączy środki ramion, jeśli tak, to informacja o trapezie równoramiennym jest zbędna.
9 lut 13:48
Jasiek:

9 lut 13:59


 Mamy już udowodnione takie twierdzenie
Twierdzenie :
Odcinek łączący środki dowolnych dwóch boków trójkąta jest równoległy do boku trzeciego i równy
jego połowie.
Mamy do udowodnienia twierdzenie
Twierdzenie:
Linia środkowa trapezu jest równoległa do obu podstaw i równa połowie sumy tych podstaw.
AB=a
CD=b
EF=r
Założenie ;
EF jest linia srodkową trapezu (czyli DE=DA i CF=FB )
Teza:
Mamy już udowodnione takie twierdzenie
Twierdzenie :
Odcinek łączący środki dowolnych dwóch boków trójkąta jest równoległy do boku trzeciego i równy
jego połowie.
Mamy do udowodnienia twierdzenie
Twierdzenie:
Linia środkowa trapezu jest równoległa do obu podstaw i równa połowie sumy tych podstaw.
AB=a
CD=b
EF=r
Założenie ;
EF jest linia srodkową trapezu (czyli DE=DA i CF=FB )
Teza:
 |AF|=a−b
|AF|=a−b

