trygonometria
smog8: wiedząc ze ctg alfa=4 oblicz wartośc wyrażenia 3(cos3 alfa − sin3 alfa)
2 kwi 13:51
M:
9 lut 09:49
Goblin:
ctgα=4 α jest kątem ostrym
cos
3α−sin
3α=(cosα−sinα)(cos
2α+cosα*sinα+sin
2α)=(cosα−sinα)(1+cosα*sinα)
{cos
2α+sin
2α=1
cosα=4sinα
(4sinα)
2+sin
2α=1
17sin
2α=1
cosα=
√1−sin2α
| | 16 | | 4 | | 4√17 | |
cosα=√ |
| = |
| = |
| |
| | 17 | | √17 | | 17 | |
3(cosα−sinα)(1+cosα*sinα)=
| | 4√17 | | √17 | | 4√17 | | √17 | | 3√17 | | 357 | |
=3( |
| − |
| )(1+ |
| * |
| )=3* |
| * |
| = |
| | 17 | | 17 | | 17 | | 17 | | 17 | | 289 | |
| | 9√17 | | 357 | | 189√17 | |
= |
| * |
| = |
| |
| | 17 | | 289 | | 289 | |
9 lut 10:49
Pick:
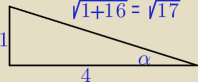
α ∊ (0
o, 90
o), ctgα = 4
| | 64 | | 1 | | 63 | |
cos3α − sin3α = |
| − |
| = |
| i już  |
| | 17√17 | | 17√17 | | 17√17 | |
no i jeszcze mnożenie otrzymanego wyniku przez 3, ale po co?

9 lut 12:54
Zuzanna:

9 lut 13:00
Goblin:
Skoro sie bawimy to inaczej
| | 1 | | 1 | | √17 | |
sinα= |
| = |
| = |
| |
| | √1+ctg2α | | √17 | | 17 | |
| | ctgα | | 4 | | 4√17 | |
cosα= |
| = |
| = |
| |
| | √1+ctg2α | | √17 | | 17 | |
Tylko zrobić teraz obliczenia
Godz 12 : 54 nie została usunięta niewymierność z mianownika.
9 lut 14:00
Ptok:
Nie ma potrzeby usuwania niewymierności z mianownika
9 lut 16:09
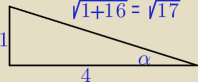 α ∊ (0o, 90o), ctgα = 4
α ∊ (0o, 90o), ctgα = 4


