BC
mm:
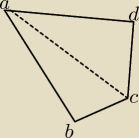
Oblicz dł. odcinka BC.
Ta figura jest wpisana w okrąg (tylko nie umiem jej tu namalować)
Odcinki
AD = 20
DC = 15
AB = 24
1 kwi 22:06
Saizou : trójkąty ABC i ACD są prostokątne
1 kwi 22:17
Saizou : oj mój błąd złe założenie sobie przyjąłem
1 kwi 22:21
mm: 18

?
1 kwi 22:23
Eta:
W tym zad. dwa razy z tw. Pitagorasa
1/ |AC|2= 202+152 ⇒ |AC |= 25
|BC|2= |AC|2−|AB|2 ⇒|BC|=..........
1 kwi 22:25
Saizou : ale tam są kąty proste, bo odcinek AC nie musi przechodzić przez środek okręgu
1 kwi 22:27
Eta:
Tak, na rys. w tym zadaniu |AC| = 2r ( mam ten test

1 kwi 22:28
Mateusz:
Z Pitagorasa to jedziesz |AC|2= |AD2|+|DC|2 to |AC|=....?
pozniej podobnie z BC |BC|2=.....?
1 kwi 22:28
Saizou : to zmienia postać rzeczy
1 kwi 22:29
asdf: mm, |AC| to średnica?
1 kwi 22:32
Eta:
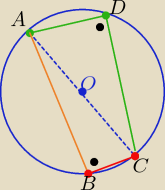
1 kwi 22:32
asdf: No to, jeżeli tak jest jak Eta narysowała to |BC|2 = √202 + 152 − 242, tak?
1 kwi 22:36
mm: Dzięki Eta

i Saizou
1 kwi 22:40
mm: AC średnica
Ale nie do końca taki rysunek
1 kwi 22:44
mm: Trochę inny test mamy

Eta
1 kwi 22:45
Eta:
Test info ?
Ważne,że |AC|=2r −−− średnica
1 kwi 22:47
mm: Ja mam podane ze AC jest średnicą okręgu tyle.
1 kwi 22:48
Eta:
No i ok

1 kwi 22:54
 Oblicz dł. odcinka BC.
Ta figura jest wpisana w okrąg (tylko nie umiem jej tu namalować)
Odcinki
AD = 20
DC = 15
AB = 24
Oblicz dł. odcinka BC.
Ta figura jest wpisana w okrąg (tylko nie umiem jej tu namalować)
Odcinki
AD = 20
DC = 15
AB = 24
 ?
?


 i Saizou
i Saizou
 Eta
Eta
