stereometria + optymalizacja psik: Pomoże ktoś z zadaniem? Rozważmy rodzinę ostrosłupów prawidłowych czworokątnych o krawędzi bocznej a. Wyznacz ten ostrosłup z podanej rodziny który ma największe pole pow. całkowitej i wyznacz to pole. Mój tok rozumowania jest taki: Skoro prawidłowy to w podstawie jest kwadrat albo romb przy czym romb raczej byłby tu niemożliwy, nie mielibyśmy jak obliczyć wysokości, nie mamy kątów. Podstawa musi być figurą foremną czyli skłaniam się ku kwadratowi. Wiem że muszę obliczyć H i wyrazić wszystko przez a. Odpowiedź powinna wynosić : P = 2a²(√2+1). Liczę na pomoc, dziękuję

Mila: Przeczytaj definicję ostrosłupa prawidłowego! W podstawie może być tylko i wyłącznie kwadrat (w tym zadaniu). Licz.

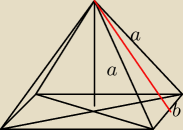
krystek: Prawidłowy w podstawie ma wielokat foremny (kąty i boki równe) czyli .... wyznacz P_p w zależności od a (jest to zadanie na ekstremum)

Mila: Cześć, Krystek,ładny rysunek. Ja udał się serniczek?

psik: To co narysowałeś rozumiem, rozumiem też czemu kwadrat, ale jak mam przedstawić Pole podstawy od a? Z wysokością wtedy bym sobie poradził. Napisze ktoś?

psik: Mógłbym za pomocą tw. cosinusów ale musiałbym wprowadzić sobie pewien kąt α, w odpowiedzi nie ma kątów.

psik:

psik: Może to ktoś wyliczyć?

krystek: Witaj MilaSerniczek , troche się przypalił, wiadomo dlaczego, ale wnuk i tak twierdzi ,że najlepszy na świecie .

krystek: Wyraź b przy pomocy a i podstaw .Zapisz sprawdzę.

Mila: To dobry pomysł z kątem. α− kąt miedzy krawędziami bocznymi, przy wierzchołku.

Mila:

	1
Pb=4*		*a2sinα i α<?180
	2

P_b=2a²sinα b²= 2a²−2a²cosα Oblicz P_c(α) funkcja osia największą wartość dla α=135

psik: jednak sobie nie radzę. Pc to b² + 3 Pściany czyli gdybym wprowadził α to Pściany = 1/2* a² * sinα. Tak czy siak muszę przedstawić b za pomocą a.

psik: jednak sobie nie radzę. Pc to b² + 3 Pściany czyli gdybym wprowadził α to Pściany = 1/2* a² * sinα. Tak czy siak muszę przedstawić b za pomocą a.

Mila: Pc to podstawa , czyli b² (policzyłam), oraz 4 ściany! boczne , (też policzyłam). Zapisz tę sumę i przyjrzyj się jej.

psik: Mila wszystko dobrze tylko czy Pc nie będzie równe wtedy Pb + b² czyli 2a²sinα +2a² − 2a²cosα i dla α = 135 Pc = 2a²cos45 + 2a² + 2a²sin45 i sin45 = cos 45 = √2/2 wtedy Pc = 2a²√2 + 2a² = 2a²(√2 +1). Och ależ to dobry wynik! A czemu α=135?

Mila: P_c=2a²(1−cosα+sinα) wyrażenie ma największą wartość gdy f(x) =(1−cosα+sinα) osiąga największą wartość dla α=135. Odczytałam z wykresu.Można ten wzór przekształcić i znaleźć największą wartość. spróbuj przekształcić.

Mila: P_c dobrze policzyłeś. Wyszedł mi wzór f(x)= √2sin(α−π/4)+1 sin(α−π/4)=1 wtedy wyrażenie ma największą wartość, stąd α=135⁰