 Promień podstawy stożka jest równy 3√2 przez wierzchołek i cieciwe podstawy
stożka o długości 6 poprowadzono płaszczyzne Otrzymany przekrój jest trójkatem równoramiennym
o kącie miedzy ramionami równym 60o Oblicz cosinus kąta nachylenia płaszczyny przekroju do
płaszczyzny podstawy stożka
wyszło mi cos=√2−1
Promień podstawy stożka jest równy 3√2 przez wierzchołek i cieciwe podstawy
stożka o długości 6 poprowadzono płaszczyzne Otrzymany przekrój jest trójkatem równoramiennym
o kącie miedzy ramionami równym 60o Oblicz cosinus kąta nachylenia płaszczyny przekroju do
płaszczyzny podstawy stożka
wyszło mi cos=√2−1
| √3 | ||
mi | ale liczyłem w pamięci i mogłem się pomylić. | |
| 3 |
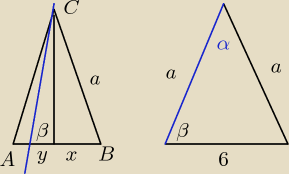 x=3√2 x+y=6 α=60o
no wiec "a" mozna łatwo policzyc z tw. cosinusów potem H i moje pytanie czy mam wyznaczyc kąt
β
x=3√2 x+y=6 α=60o
no wiec "a" mozna łatwo policzyc z tw. cosinusów potem H i moje pytanie czy mam wyznaczyc kąt
β
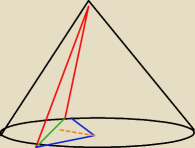 zielony to cięciwa i ma długość 6. Zatem bez problemu możemy policzyć wysokośc trójkąta zielono
czerwonego : h = 3√3.. Później z twierdzenie Pitagorasa udowadniamy że trójkąta niebiesko
zielony jest prostokątny i liczymy jego wysokość : h2 = 3
zielony to cięciwa i ma długość 6. Zatem bez problemu możemy policzyć wysokośc trójkąta zielono
czerwonego : h = 3√3.. Później z twierdzenie Pitagorasa udowadniamy że trójkąta niebiesko
zielony jest prostokątny i liczymy jego wysokość : h2 = 3
| h2 | √3 | |||
na koniec cosγ = | = | |||
| h | 3 |
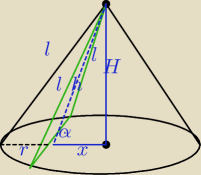
| l√3 | ||
H2=l2−r2, przekrój jest trójkątem równobocznym, l=6, h= | ||
| 2 |
| x | ||
cosα= | ||
| h |
