. Krzysiek: Punkt P leży wewnàtrz prostokąta ABCD. Wykaż, że suma pól trójkątów APD i BPC jest równa sumie pól trójkątów APB i DPC.

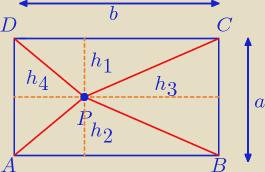
rumpek: 1^o Trójkąty APB i DPC mają równe podstawy oraz różne wysokości. h₁ + h₂ = a

	1
PAPB =		* b * h2
	2

	1
PDPC =		* b * h1
	2

	1		1
PAPB + PDPC =		* b * h2 +		* b * h1
	2		2

	1
PAPB + PDPC =		* b(h2 + h1)
	2

	1
PAPB + PDPC =		* a * b
	2

2^o Trójkąty APD i BPC mają równe podstawy oraz różne wysokości. h₃ + h₄ = b

	1
PAPD =		* a * h4
	2

	1
PBPC =		* a * h3
	2

	1		1
PAPD + PBPC =		* a * h4 +		* a * h3
	2		2

	1
PAPD + PBPC =		* a(h4 + h3)
	2

	1
PAPD + PBPC =		* a * b
	2

P_APD + P_BPC = P_APB + P_DPC c.n.u. należą się dwa jabłka