. DSGN.: Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami o przyprostokątnych długości 12cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.

Mila: Z czym masz problem?

DSGN.: sciany boczne są trójkatami równoramiennymi czyli 12 to jest wysokość trojkata rownoramiennego czy jak nie wiem gdzie obsadzić tą 12

Mila: Są też Δ prostokątnymi. Zatem to wygląda jak ścięte naroże sześcianu. Oblicz i podaj wynik.

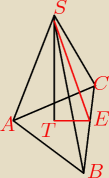
maddhew: kąt ASB jest prosty |SA|=|SB|=12 ⇒ |AB|=12√2 P_p=72√3 P_b=144*3/2 = 216 |ST|=H |SE|=h h=√144−(6√2)² = 6√2 H²=h²−|TE|, |TE| to 1/3 wysokości podstawy. Dokończ

Mila: Można tak, ale widzę prostszy sposób.

DSGN.: własnie probowałem tak jak Maddhew i chyba tylko w obliczeniach sie trzasnąłem a Mila Twojego sposobu nie widze (moze juz jestem zmeczony, albo ograniczony )

Mila: No to postaw, ten ostrosłup na bocznej ściance, jak naroże sześcianu.

	1		1
V=		*(		*12*12)*12
	3		2

taka odpowiedź?

DSGN.: Mila zgadza się

Mila: Czy już rozumiesz na czym to polega?

DSGN.: to zadanie teraz tak poćwieczę jutro z innymi, zobaczymy jak to bd szło