f Pomocy: Stożek, w którym promień podstawy ma 8 cm długości, a wysokość 24 cm, przecięto płaszczyzną równoległą do podstawy stożka. Odległość płaszczyzny przekroju o wierzchołka stożka jest równa 6 cm. Oblicz objętość obu części stożka.

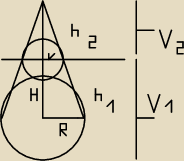
Ryuuk: H = 24 R = 8 h₂ = 6 h₁ = 18 Obliczam "r" ze wzoru H = (h₁ * R) / (R − r) 24 = (18 * 8) / (8 − r) 24 = 144 / (8 − r) r = 2 V₁ = 1/3 pi (nie wiem jak narysować ) 18 * (64 + 16 + 4) = 1/3 pi * 18 * 84 = 504 pi Objętość ściętego stożka wynosi 504 pi V₂ = 1/3 pi * r² * h₂ V₂ = 1/3 pi * 4 * 6 V₂ = 8 pi Objętość drugiego stożka wynosi 8 pi. wzory z których korzystałem: − Wysokość stożka przed ścięciem: H = (h * R) / (R − r) Jak są pytania to proszę pisać

u: H = (h1 * R) / (R − r) czemu taki wzór ?

Ryuuk: Jest to wzór na wysokość stożka przed ścięciem. Z niego obliczyłem "r" bo jest jedyną niewiadomą.

u: nigdy nie widziałam takiego wzoru. Skąd go wziąłeś ?

Ryuuk: Ze szkoły

u: ja tez zadanie zrobiłam troszeczkę inaczej ale wynik wyszedł mi taki sam. (mnie nie uczono w szkole takich wzorów )

Ryuuk: wyższa szkoła jazdy grunt że taki sam wynik

u: eee ja tez chcem poznawac w szkole takie wzory xD