. DSGN.: W ostrosłupie prawidłowym czworokątnym α jest kątem nachylenia ściany bocznej do płaszczyzny podstawy a β katem miedzy krawedzią boczna a krawedzia podstawy ostrosłupa

	1
Wykaz ze sin2α+		=2
	sin2β

wielkie dzięki

Godzio: Coś nie tak w tej zależności hmmm

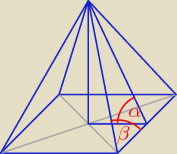
Godzio: h − wysokość ściany bocznej a − krawędź podstawy

	1   a 2		a
cosα =		⇒ cosα =
	h		2b

	1   a 2		a
ctgβ =		⇒ ctgβ =
	b		2b

Dzieląc oba równania przez siebie otrzymamy:

cosα
	= 1 /2
ctgβ

	cos2β
cos2α =
	sin2β

	1 − sin2β
1 − sin2α =
	sin2β

	1
sin2α +		= 2 co kończy dowód
	sin2β

Źle przeczytałem polecenie na początku...