funkcje blogther: mamy podana funkcje y = | ¹₂x − 2 |

	|f(x)|
zapisz wzor funkcji h(x) =		bez uzycia symbolu wartosci bezwzglednej i narysowac
	f(x)

jej wykres

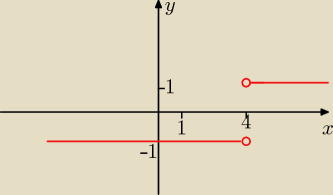
Eta: dla x >4 dla x <4 f(x) = 1 f(x)= −1

krystek: dla x≥4 mamy h(x)=1 dla x<4 mamy h(x)=−1 poniewaz I¹₂x−2I=−(¹₂x−2)

krystek: Witaj ,−ku.

Eta:

krystek: A i mam JEDYNKĘ< dzięki Eta jak zawsze na straży!

blogther: to co wam podałem to jest tylko czesc funkcji f(x) bo myslałem ze jak dam wam czesc do zrozumiem jak to sie robi ale jak widze to nie moge tego tak od razy pokapowac wiec jak nic nie wymysle to podam wam cała funkcje f(x) ale to za chwile

blogther: czyli 4 to miejsce zerowe tak a −1 i 1 to skad sie wzieło?

ZKS: A w którym miejscu ta funkcja przecina oś X w punkcie 4 że mówisz że to miejsce zerowe?

krystek: A widzisz gdzieś miejsca zerowe?

blogther: okey pokaze wam jak ja to rozwiazałem majac pełna funkcje f(x)

krystek: I doczekać się nie mogę!

pigor: ... otóż z warunków zadania :

	|f(x)|		||12x−2||
f(x)= |12x−2| ⇒ g(x)=		=		=
	f(x)		|12x−2|

	|12x−2|
=		=1 ⇔ 12x−2|≠0 ⇔ 12x−2≠0 ⇔ x≠4. a więc
	|12x−2|

g(x)=1 , gdy x≠4 i to wszystko . ...

pigor: ... oczywiście w przedostatniej linijce zamiast ¹₂x−2|≠0 miało być |¹₂x−2|≠0 , bo skracałem przez "to to" . ...

krystek:

blogther: f(x) = | ¹₂x + 2 | + | ³₂x − 3 | − 5

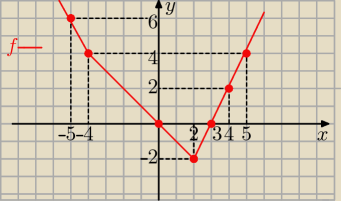
	⎧	−2x−4 dla x∊(−∞,−4)
f(x) =	⎨	−x dla x∊<4;2>
	⎩	2x−6 dla x∊(2; +∞)

czy dobrze zaznaczyłem przedziały chodzi mi o to czy jest domkniety czy otwarty? czy moze tak byc jak ja to zrobiłem czy tak to ma byc chodzi mi o wykres? yx211

blogther: tam po dodatniej stronie x−ow gdzie sa na ujemnych y zamolwane kołeczko na na dodatnich y otwart kołeczko powinno byc 2 ale nie wiem czemu sie nie wyswietliło

krystek: A jak wygląda wykres y=−2x−4

krystek: Pytanie na początku Twojego postu ma się nijak do tego co teraz podałeś.

blogther: no bo to był tylko przykład zebym wiedział jak rozwiazac ten własciwy nie chciałem isc na łatwize i dawac wam zebyscie zamnie rozwiazali tylko dałem prostszy zeby wiedziec jak postepowac teraz juz wiesz po co to zrobiłem

blogther: ale dobrze to robie

Aga1: Drugi przedział <−4,2), a trzeci <2,∞) Twój wykres na pewno nie jest wykresem funkcji, którą poniżej dobrze rozpisałeś .

blogther:

blogther: wykres tak powinien wygladac?

blogther: a dlaczego takie przedziały bo nie wiem skad sie to bierze?

blogther: moze ktos mi pomoc?

Eta:

blogther: tak ale chodzi mi o to:

	|f(x)|
zapisz wzor funkcji h(x) =		bez uzycia symbolu wartosci bezwzglednej i narysowac
	f(x)

jej wykres funkcja f(x) = | ¹₂x + 2 | + ³₂x − 3 | + 5 wyzej wyznaczyłem juz przedziały i narysowałem wykres dwa czy ten drugi jest poprawny? i dlaczego takie sa przedziały jak podała AGA1 bo ja nie wiem dlaczego takie skad sie to wziało moze mi to ktos wytłumaczyc i jakos ładnie rozpisac?

blogther: ?

Aga1: W ostatnim poście umieściłeś dwa zadania W pierwszym zadaniu mianownik różny od zera, więc oba przedziały są otwarte. W drugim np. z definicji

	1		1		1
I		x+2I=		x+2, gdy		x+2≥0⇒x≥−4 ⇒x∊<−4,∞)
	2		2		2

	1		1		1
I		x+2I=−(		x+2, gdy		x+2<0⇒x∊(−∞,−4).
	2		2		2

Jak nabierzesz wprawy, to zauważysz pewną prawidłowość. Wykresy narysowała Eta.