rownanie kwadratowe z wartoscia bezwzgledna gosia: |x²−x|+|x+1|=x²−2x−1 rozwiaz rownanie i zdefiniowalam obie wartosci i mam x²≥x x²<x x≥−1 x>−1 i nie wiem co dalej, moze mam blad gdzies w definicji?

Aga1: Ix²−xI=x²−x, gdy x²−x≥0⇔x(x−1)≥0⇔x∊(−∞,0>∪<1.∞) Ix²−xI=−x²+x, gdy x∊(0,1) Ix+1I=x+1, x+1≥0⇔x∊<−1,∞) Ix+1i=−x−1, gdy x<−1 Rozpatrujesz przypadki 1. x<−1 x²−x−x−1=x²−2x−1 0=0 Rozwiązaniem jest każda liczba z przedziału (−∞, −1) 2. x∊<−1,0) x²−x+x+1=x²−2x−1 licz

gosia: ok dziękuje !

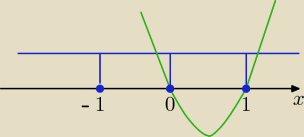
Eta: Założenie 1/ po prawej stronie musi być :x²−2x−1 ≥0 rozwiąż tę nierówność otrzymasz x€ ( −∞, 1−√2> U <1+√2,∞) Miejsca zerowe pod modułami x²−x= x(x−1)=0 x=0 v x= 1 i x= −1 rozpatrz teraz równanie przedziałami

Aga1: Eta, jeśli rozwiązujemy z przypadkami to koniecznie musimy zapisać założenie o prawej stronie?

Eta: @Aga1 Nie jest to konieczne , ale też nie zaszkodzi ( ja zawsze tak piszę z "rozpędu" Pozdrawiam