a jasio: Dana jest funkcja kwadratowa f(x)=¹₂x²−2:

	|f(x)|
a) Narysuj wykres funkcji g(x)=		, której dziedziną jest zbiór
	f(x)

(−5, −2) U (−2, 2) U (2, 5). b) Zapisz zbiór rozwiązań nierówności g(x)<0 Nie bardzo wiem jak zabrać się za podpunkt a, liczę na wasza pomoc

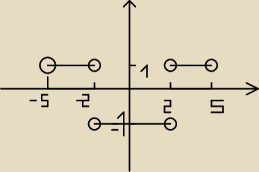
Eta: Witam Jasiu Rozpatrujemy wykres g(x) przedziałami: f(x)= ¹₂x² − 2 miejsca zerowe f(x) to ¹₂x² − 2=0 <=> x² − 4=0 <=> x= 2 v x= −2 czyli dla x€(−∞, −2> U <2,∞) −−− f(x) ≥0 dla x€ ( −2, 2) −−−−− f(x) <0 więc 1/ dla x€(−∞, −2) U ( 2,∞) bo D_g: x€R − {−2, 2} mamy : ¹₂x² −2 g(x) = −−−−−−−−−−−−− ¹₂x² − 2 czyli g(x) = 1 podobnie : dla: 2/ x€(−2,2) g(x)= −1 wykres g(x) masz narysowany ! zad b) g(x) <0 widzisz na wykresie ,że wtedy x€ ( −2, 2)

jasio: hm, nie rozumiem tylko tej części: więc 1/ dla x€(−∞, −2) U ( 2,∞) bo Dg: x€R − {−2, 2} mamy : ¹₂x² −2 g(x) = −−−−−−−−−−−−− ¹₂x² − 2 Czy ta wartosci bezwzgledna nic nie zmienia?

Eta: Nie zmieniasz znaku f(x) bo wartości pod modułem >0 ale nie moga być =0 bo masz f(x) w mianowniku więc dla mianownika x ≠2 x≠−2 czyli D: x€R− {−2,2} dla x€(−2,2) po opuszczeniu modułu zmieniasz znak czyli w liczniku masz −( f(x))

jasio: juz kapuje, dzieki