kwadrat hektor: W kwadrat ABCD o boku 2a wpisano okrąg. Oblicz długość cięciwy wyciętej przez ten okrąg z odcinka łączącego wierzchołek A ze środkiem boku CD .

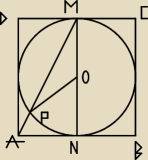
Basia: kat DAM = kąt AMO = α OM = OP = a kat OPM = kąt OMP = α ⇒ kąt POM = 180−2α z tw.cosinusów MP² = OP² + OM² − 2*OP*OM*cos(180−2α) MP² = a² + a² − 2*a*a*(−cos2α) MP² = 2a² + 2a²*cos2α z tw.Pitagorasa AM² = AD² + MD² AM² = (2a)² + a² AM² = 4a² a² AM² = 5a² AM = a√5

	MD		a		1		√5
sinα =		=		=		=
	AM		a√5		√5		5

	AD		2a		2		2√5
cosα =		=		=		=
	AM		a√5		√5		5

	4*5		5		4		1		3
cos(2α) = cos2α − sin 2α =		−		=		−		=
	25		25		5		5		5

MP² = 2a² + 2a²*cos2α MP² = 2a²(1+cos2α)

	3		8		16a2
MP2 = 2a2(1+		) = 2a2*		=
	5		5		5

	4a√5
MP = U{4a}{√5 =
	5

Eta: Można też tak:( myślę ,że prościej) Nawiązuję do oznaczeń z rys, Basi ΔMPN −− jest prostokatny bo NM−−to średnica okręgu więc kąt MPN = 90^o zatem ΔAMN ~ ΔMNP czyli: ^IPMI_IMN= ^IMNI_IAMI przekształcając mamy: IPMI =^IMNI2_IAMI gdzie IMNI= 2a => IMNI² = 4a² z tw. Pitagorasa IAMI =√a² +4a² zatem: IPMI = ^4a2_√5a² to IPMI = ^4a_√5 to IMNI = ^4a√5₅ wynik oczywiście ten sam

Eta: Oczywiście w ostatnim IPMI= ^4a√5₅ Dobranoc!