Proszę o pomoc tomek:

	x
Dla jakich p równanie p=|		| ma 1 rozw.
	x−1

Mila: Rozwiąż graficznie.

	x−1+1		1
1) f(x)=		=		+1
	x−1		x−1

Narysuj wykres f(x) 2) narsuj wykres |f(x)| 3) sprawdz ile punktów wspólnych ma otrzymany wykres z poziomą prostą y=p

tomek: wyszedł mi jeden punkt dla y=0 dobrze?

Mila: dla p=0? Narysuję , to odpowiem, ale po 20.

tomek: a mogłabyś teraz proszę

tomek: mógłby ktoś to sprawdzić?

MQ: Wychodzi p=0 i p=1

tomek: czemu p=1?

Basia:

	x
|		| = p
	x−1

D: x∊R\{1}

x		x
	= p lub		= −p
x−1		x−1

x = p(x−1) lub x=−p(x−1) x = px − p lub x = −px + p x − px = −p lub x+px = p (1−p)*x = −p lub (1+p)*x = p 1. p=1 0*x = −1 sprzecznośc 2*x = 1 x = ¹₂ czyli dla p=1 jest jedno rozwiązanie 2. p = −1 2x = 1 x = ¹₂ 0*x = −1 sprezeczność czyli dla p = −1 też jest jedno rozwiązanie 3. p≠1 i p≠ −1 wtedy

	−p		p
x =		lub x =
	1−p		1+p

czyli są wtedy dwa rozwiązania, no chyba, że dla jakiegoś p te ułamki są równe

−p		p
	=
1−p		1+p

−p(1+p) = p(1−p) −p − p² = p − p² −p = p a to jest prawdą dla p=0 czyli także dla p=0 mamy jedno rozwiązanie Odp. p= −1 lub p=0 lub p= −1

MQ:

tomek: dziękuję

Basia: oczywiście p = −1 odpada, bo wartość bezwzględna nie może być ujemna; zawsze czegoś zapomnę dopisać

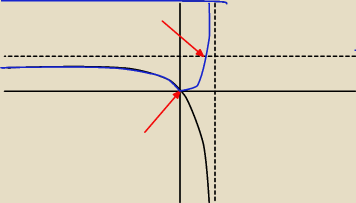
MQ: Ta druga gałąź nie chce mi wyjść na rysunku. Powinna być ładna hiperbola w prawej górnej ćwiartce osi przerywanych, jak czarna, tylko symetrycznie względem punktu przecięcia osi przerywanych

MQ: Dolny punkt (0,0) górny punkt (¹₂, 1)

Basia: te łuki czasem robią takie głupie kawały i "nie ma mocnych"

Mila: Jestem już.Patrz na wykres. Prosta y=0 i prosta y=1 przecina wykres w jednym punkcie. Odp. Dla p=0 i dla p=1 równanie ma jedno rozwiązanie.