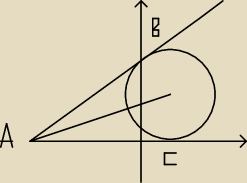
Dwie styczne do okręgu w układzie współrzędnych. Znajdz wzór stycznej BigMax: Okrąg przedstawiony na rysunku jest styczny do osi OX w punkcie ( 2,0), a prosta k przechodzi przez punkt A = ( −6,0) i jest styczna do okręgu w punkcie B. Znajdź równanie stycznej k wiedząc że punkt A znajduje się w odległości 6√2 od środka okręgu? −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− Obliczyłem równanie prostej zawierającej odcinek BC, ale teraz nie mam pomysłu na to by wmiare prosty sposób znaleźć punkt B by obliczyć tą prostą. Proszę o własne przemyślenia co do tego zadania. Z góry dziękuje Ps. Punkt B nie leży na osi OY. Tak mi się narysowało. Na rysunku w książce B jest delikatnie po prawej stronie osi OY

Basia: S − środek okręgu S(2,y_s) AS = 6√2 z tego wyliczysz y_s mając y_s możesz napisać równanie okręgu masz już pr.BC czyli układ równań

Basia: albo symetria osiowa względem pr.AS, ale tego w szkole chyba teraz nie ma (bo B i C są symetryczne względem AS)

Bogdan: Punkty A i B są punktami wspólnymi okręgu narysowanego i okręgu o środku A i promieniu równym 6√2, czyli okręgu (x + 6)² + y² = 72

Bogdan: Poprawka, nie punkty A i B, a punkty B i C

aga: S ma współczesne (2,3), podstawiamy do równania y = ax+b punkt A(−6,0) i wychodzi ax+y+6a=0, potem liczymy : w wartości bezwzględnej(2a+3−6a) podzielić przez pod pierwiastkiem: a do kwadratu + 1 a to wszystko sie równa 2 pierwiastki z 2, i wychodzi nam a=0 i a= 4pierwiastki z 2 a końcowe równanie to y= 4pierwiastki z 2−7y+24pierwiastki z 2.