matematykaszkolna.pl
planimetria kora: pomóżcie W trójkącie ABC środkowa AD jest prostopadła do boku AC . Kąt BAC ma miarę 120∘ . Wykaż, że |AB | = 2|AC | .
29 mar 14:14
Ted: ... gdzie jest bła
29 mar 14:22
kora: tzn
29 mar 14:43
Mila: Środkowa AD może być prostopadła do boku BC.
29 mar 14:46
kora: właśnie. rysunek już mam, tylko jak to udowodnic?
29 mar 14:47
Mila: Popraw treść zadania, bo jest bez sensu.
29 mar 14:50
rumpek: Mila treść jest ok emotka emotka
29 mar 14:52
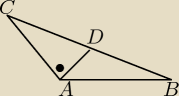
Ajtek: rysunekTak to mniej więcej wygląda, w pierwszej chwili rownież myślałem iż jest błąd emotka.
29 mar 14:56
rumpek: https://matematykaszkolna.pl/forum/133274.html już je robiłem − na tej stronie rysunek a gdzieś dałem rozwiązanie emotka
29 mar 14:57
Mila: OK
29 mar 14:57
Mila: No cóż, do schematów człowiek się przyzwyczaja, fajne zadanko. Kora znalazłaś rozwiązanie podane przez Rumpka?
29 mar 15:01
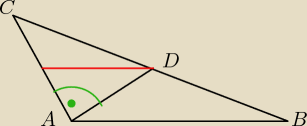
Ted: rysunek Środkowa dzieli trójąt na dwa o równych polach ....dalej już z górki −emotka
29 mar 15:09
rumpek: łatwiej tw. sinusów emotka
29 mar 15:10
Mila: Kora?
29 mar 15:13
kora: niestety, nie mam pomysłu nadal :<
29 mar 15:15
Mila: Kąt DAB=300
1 1 
AC*AD=
*AD*c*sin30
2 2 
29 mar 15:15
kora: co to jest c?
29 mar 15:26
Mila: AB (bok leżący naprzeciw wierzchołka C), tam porównanie pól. ?
29 mar 15:27
kora: dzięki emotka
29 mar 15:31
Mila: Podziękuj Rumpkowi, Tedowi i Ajtkowi, bo wyprowadzili mnie z błedu co do treści .
29 mar 15:34
kora: dzięki wam wszystkim
29 mar 16:03
ainsztain: γ∞≥≥⊂←≈∑δ≠←∫⊂≥≤ΩπΔδ zasada Kornela Defogla
29 mar 17:49
Mila: Licz na nas.emotka
29 mar 20:09