funkcja logarytmiczna Paweł: Wyznacz dziedzinę funkcji

	1
g(x)=log		−4x (2x2−3x+1)
	3

1
	−4x − to podstawa logarytmu
3

Ajtek:

	1
{		−4x>0
	3

	1
{		−4x≠1
	3

{2x²−3x+1>0 Dziedziną jest część wspólna tych przedziałów.

Eta: log_ab to D: a>0 i a≠1 i b>0

Paweł: sory Ajtek złe zadanie przepisałem nie wiem tego

	x2+1
log12
	2−3x

Paweł: wychodzi mi że D to zbiór pusty

Lekarzyk: 2−3x≠0 −3x≠−2 x≠²₃ x∊R/²₃

Paweł: Lekarzyk napewno ? a inne założenia ?

Ajtek: Rozwal nierówność:

x2+1
	>0
2−3x

	x2+1
Jeżeli		to liczba logarytmowana .
	2−3x

Ajtek: no i oczywiście 2−3x≠0

Paweł: no i właśnie Ajtek wychodzą mi chore rzeczy

Ajtek: tzn?

Paweł: D=zbiór pusty

Ajtek: jak zbiór pusty? Pokaż obliczenia

Paweł:

x2+1
	>0 / (2−3x)2
2−3x

(x²+1)(2−3x)>0 nie mam miejsc zerowych w pierwszym nawiasie w drugim też bo są założenia a₃=−3 więc wykres zaczynam rysować z dołu z prawej strony i on nigdy nie przejdzie osi ox więc dla żadnego x (x²+1)(2−3x)>0

Ajtek:

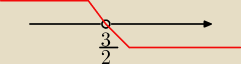
	3
śpiący już jestem ale jak dla mnie dziedzina to (−∞;		)
	2

3

Tragos: ohoho... (x²+1)(2 − 3x) > 0 (mnożymy przez x² + 1, zawsze dodatnie) i 2 − 3x ≠ 0 2 − 3x > 0 i 2 − 3x ≠ 0 2 − 3x > 0 x ∊ ......

Paweł:

	2
w odpowiedziach jest do		a to u góry to skąd wziąłeś ?
	3

Ajtek:

	2
Cholera		miało byc oczywiście
	3

Paweł: Tragos tam chyba miało być że dzielisz przez x²+1 i tak sobie można dzielić ?

Tragos: no dzielę, dzielę tutaj wolno bo x² + 1 jest zawsze dodatnie

Ajtek: W tym przypadku można ponieważ x²+1 nigdy nie będzie równe 0.

Paweł: chore zadanie

Ajtek: i zawsze dodatnie