prawdopo
gryzdek: 
Scianki kostki do gry oznaczono liczbami −3 , −2, −1, 0, 1, 2, 3 Jakie jest
prawdopodobieństwo że przy dwukrotnym rzucie tą kostką uzyskamy sumę oczek większą od 1?
maddhew: Ω=7
2=49
A − wylosowano sumę oczek > 1
A = {(−1,3), (0,2), (0,3), (1,1), (1,2), (1,3) (2,0), (2,1), (2,2), (2,3), (3,−1), (3,0),
(3,1), (3,2), (3,3)}
Jeśli w którymś rzucie wypadło −3 lub −2 to nie da się uzyskać sumy oczek większej od 1.
Tak więc moc A to 15.
P(A)=
1549
A na przyszłość polecam drzewko stochastyczne, wszystkie zadania z poziomu liceum da się za
jego pomocą rozwiązać
maddhew:
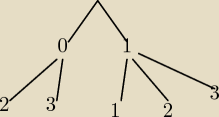
Oczywiście, że się da. Roboty nie jest tak dużo, jeśli przy rysowaniu odrzuci się od razu
zbędne gałęzie. Powyżej macie fragment takiego drzewka dla 0 i 1 w pierwszym rzucie, tylko
zdarzenia spełniające warunek są uwzględnione. Prawdopodobieństwo każdej krawędzi to
17,
czyli całej gałęzi
149
maddhew: Saizou nigdzie nie masz napisane, że kostka jest sześcienna, sam bawiłem się kostkami 7,8,12,20
ściennymi
Saizou : pierwsze słyszę o kostkach 7,8,12,20 ściennych
? kurcze nie wiem