geometria, typu uzasadnij Roz: W trójkącie ABC na boku AB obrano punk M (M≠A, M≠B). Punkty K i L sa odpowiednio środkami boków AC i BC. Uzasadnij, że pole czworokąta KMLC jest równe sumie pól trójkątów AMK i MBL.

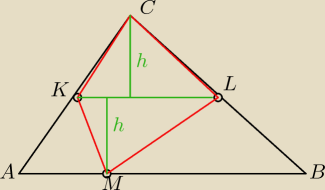
Ted: 2IKLI=IABI

	IAMIh		IBMIh		hIABI
SΔAMK+SΔBLM=		+		=
	2		2		2

	IKLIh		hIABI
S□KMLC=2		=IKLIh=
	2		2

Roz: czemu 2KL = AB ?

Ted: z twierdzenia Talesa −

Ted: albo podobieństwa trójkątów

pigor: ... lub połącz M z wierzchołkiem C , a wtedy z równości par pól (równe podstawy i wysokości względem nich) trójkątów ; P_ΔMBL=P_ΔMLC i P_ΔMAK=P_ΔMKC ⇒ ⇒ P_MLCK=P_MLC+P_MKC=P_ΔMBL+P_ΔMAK . ... c b.d.u . ...