tak to widzę:
a=12
b=10
c=7
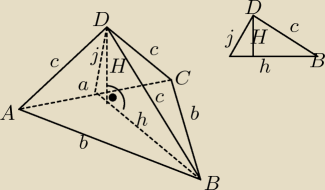
Pole boczne to suma 3 trójkątów równoramiennych. Dwóch takich samych o podstawie 10 i jednego o
podstawie 12.
Trójkąty ABD i BCD są takie same. Ich wysokości nie rysowałem, bo rysunek zrobiłby się nie
czytelny te wysokości nazwijmy k.
Chcąc je wyliczyć posłużymy się twierdzeniem Pitagorasa.
k
2=c
2−(
b2)
2 −−> k
2=49−25 −−> k
2=24 −−> k=
√24 −−>k=2
√6
Teraz wysokość j, tym samym sposobem.
j
2=c
2−(
a2)
2 −−> j
2=49−36 −−> j
2=13 −−>j=
√13
Następnie sumujemy pola tych trójkątów i mamy pole powierzchni bocznej.
Pb=2(
12*b*k)+
12*a*j
Pb=2(
12*10*2
√6)+
12*12*
√13=2*10
√6+6
√13=5
√6+6
√13
Kolejno liczymy objętość korzystając ze wzoru V=
13Pp*H
Wyliczmy najpierw h (wysokość podstawy) jest ona niezbędna do obliczenia Pola podstawy (Pp) i
wysokości ostrosłupa H. Jedziemy tak samo Pitagorasem.
h
2=b
2−(
a2)
2 −−> h
2=100−36 −−> h
2=64 −−> h=
√64 −−> h=8
Teraz wysokość ostrosłupa
H=
j*ch −−> H=
7√138
Na końcu liczymy objętość.
V=
13Pp*H −−>
13*
12*a*h*H −−>
13*48*
7√138 −−>
13*42
√13
V=14
√13
Wszystko

 a=12
b=10
c=7
Pole boczne to suma 3 trójkątów równoramiennych. Dwóch takich samych o podstawie 10 i jednego o
podstawie 12.
Trójkąty ABD i BCD są takie same. Ich wysokości nie rysowałem, bo rysunek zrobiłby się nie
czytelny te wysokości nazwijmy k.
Chcąc je wyliczyć posłużymy się twierdzeniem Pitagorasa.
k2=c2−(b2)2 −−> k2=49−25 −−> k2=24 −−> k=√24 −−>k=2√6
Teraz wysokość j, tym samym sposobem.
j2=c2−(a2)2 −−> j2=49−36 −−> j2=13 −−>j=√13
Następnie sumujemy pola tych trójkątów i mamy pole powierzchni bocznej.
Pb=2(12*b*k)+12*a*j
Pb=2(12*10*2√6)+12*12*√13=2*10√6+6√13=5√6+6√13
Kolejno liczymy objętość korzystając ze wzoru V=13Pp*H
Wyliczmy najpierw h (wysokość podstawy) jest ona niezbędna do obliczenia Pola podstawy (Pp) i
wysokości ostrosłupa H. Jedziemy tak samo Pitagorasem.
h2=b2−(a2)2 −−> h2=100−36 −−> h2=64 −−> h=√64 −−> h=8
Teraz wysokość ostrosłupa
H=j*ch −−> H=7√138
Na końcu liczymy objętość.
V=13Pp*H −−> 13*12*a*h*H −−> 13*48*7√138 −−> 13*42√13
V=14√13
Wszystko
a=12
b=10
c=7
Pole boczne to suma 3 trójkątów równoramiennych. Dwóch takich samych o podstawie 10 i jednego o
podstawie 12.
Trójkąty ABD i BCD są takie same. Ich wysokości nie rysowałem, bo rysunek zrobiłby się nie
czytelny te wysokości nazwijmy k.
Chcąc je wyliczyć posłużymy się twierdzeniem Pitagorasa.
k2=c2−(b2)2 −−> k2=49−25 −−> k2=24 −−> k=√24 −−>k=2√6
Teraz wysokość j, tym samym sposobem.
j2=c2−(a2)2 −−> j2=49−36 −−> j2=13 −−>j=√13
Następnie sumujemy pola tych trójkątów i mamy pole powierzchni bocznej.
Pb=2(12*b*k)+12*a*j
Pb=2(12*10*2√6)+12*12*√13=2*10√6+6√13=5√6+6√13
Kolejno liczymy objętość korzystając ze wzoru V=13Pp*H
Wyliczmy najpierw h (wysokość podstawy) jest ona niezbędna do obliczenia Pola podstawy (Pp) i
wysokości ostrosłupa H. Jedziemy tak samo Pitagorasem.
h2=b2−(a2)2 −−> h2=100−36 −−> h2=64 −−> h=√64 −−> h=8
Teraz wysokość ostrosłupa
H=j*ch −−> H=7√138
Na końcu liczymy objętość.
V=13Pp*H −−> 13*12*a*h*H −−> 13*48*7√138 −−> 13*42√13
V=14√13
Wszystko 