Zbiorem rozwiązań nierówności x^2+36>0 jest: Mariusz: Zbiorem rozwiązań nierówności x²+36>0 jest: Zawsze robiłem to tak, że przyrównywałem to co jest przed znakiem większość do 0 i zaznaczałem na osi liczbowej x1 i x1 i rysowałem parabolę uśmiechniętą bądź smutną i wyznaczałem zbiór. W tym wypadku wyszło mi, że x²+36=0 to x² = −36 co jest niemożliwe więc zaznaczyłem odpowiedź, że zbiór jest pusty. Okazuje się, że to jednak ponoć nie jest prawda. Że dobrą odpowiedzą jest: R Jak to rozumieć? Czy mój sposób rozwiązywania tego typu zadań jest zły?

Ajtek: NIe możesz z nierówności przejść do równania

Ajtek: x²+36>0 x²>−36 i to jest prawdą dla x∊R

Mariusz: to na przyszłosc jak rozwiązywac takie zadania? Jakbym chciał policzyć Δ, to też mi wyjdzie, że jest <0 więc nie ma rozwiązań.

Ajtek: Dokłądnie .

Beti: patrz tu:https://matematykaszkolna.pl/forum/136285.html

Ajtek: Tylko po co liczyć Δ jak na pierwszy rzut oka widać, że nierówność jest spełniona dla wszystkich x∊R.

Beti: bo nie wszyscy potrafią "rzucać okiem" niektórzy robia zad. mechanicznie (niestety)

Mariusz: rozumiem. a popatrzmy jak miałem taki przykład: x²<x to robiłem tak: x²−x<0 x(x−1)<0 i to przyrównywałem do zera, x=0 i x−1=0, więc x= 0 − x= 1 i to też źle robiłem wtedy?

Aga1: x=0 lub x=1.Tu dobrze i dalej...

Beti: robiłeś dobrze

Mila: Jeśli upierasz się przy delcie, to: 1) a=1 parabola skierowana do góry 2)Δ<0 zatem parabola nie przecina osi OX (brak miejsc zerowych) ,czyli leży nad osią ox i przyjmuje tylko wartości dodatnie dla x∊R

krystek: x=0 lub x=1 i wykres i wartości ujemne odczytujes z wykresu x∊(0,1)

krystek: https://matematykaszkolna.pl/strona/79.html

Mariusz: Mila rozumiem. Tylko, że patrzcie. w drugim przypadku , że przyrównuję lewą stronę do 0 jest ok. a a pierwszym ajtek mówi, że nie mogę przyrównać lewej strony do 0, więc kiedy ogólnie mogę a kiedy nie mogę?

Ajtek: Źle mnie zrozumiałeś, nie możesz zamienić nierówności na równanie. Natomiast przy poszukiwaniu pierwiastkow ten znak siłą rzeczy stawiamy, ale musimy pamiętać iż rozwiązaniem jest/są przedziały, a nie te dwie konkretne liczby.

krystek: zawsze możesz aby poszukać m zerowych Jak miałes x²+36 =0 to widzisz ,że Δ=−4*1*36 i nie masz miejsc zerowych . Popatrz jak wygląda wykres a>0 i Δ<0

Mila: Przyrównujesz do zera aby obliczyć miejsca zerowe (bo są Ci potrzebne) lub wykazać że ich nie ma.

Beti: przyrównujesz do zera jak obliczasz pierwiastki x₁, x₂,... a w tym przykładzie pierw. nie da sie policzyć (bo np. Δ<0)

Mariusz: rozumiem. Krystek, właśnie chcę się nauczyć bez liczenia delty, tylko tak na oko byłoby fajnie zacząć to ogarniać

Mariusz: może chcielibyście mi napisać kilka ciekawych przykładów co bym je rozwiązał sobie?

Mariusz: aha i jak by było tak: x²+36 <0 to jaka by była odpowiedź?

krystek: x²+2x+1≤0

Mariusz: w tym co mi napisałeś, wyszło, ze tylko −1 spełnia tę nierówność. Ale jak to zapisać?

krystek: Nakreśl parabolę y=x²+36 i odpowiedz na postawione pytanie

Mariusz: Krsystek, wtedy będzie chyba zbiór pusty tak? Bo wtedy żadna liczba by nie spełniała nierównośći.

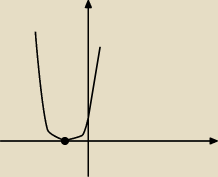
krystek: (x+1)²≤0 m zerowe x=−1

krystek: A jaka dasz odpowiedź dla nierówności x²+2x+1>0

krystek: Do poprzedniego przykładu TAK

Mariusz: x∊(−∞,−1)∪(−1,+∞), dobrze?

krystek: ok a x²+2x+1≥0

Mariusz: x∊R ?

krystek: I następne −x²−2>0

Mariusz: zbiór pusty?

krystek: ok

Mariusz: ty chyba rozumiem dziękuje Wam wszystkim, jesteście świetni

krystek: Musisz dobrze opanować wykresy trójmianu w zależności od a i Δ. Podany masz link, ponieważ na podstawie wykresu rozwiązujemy nierówności.