 1.Pole graniastosłupa prawidlowego trójkątnego jest równe 2{3}+24 cm2. Wysokość jest 2 razy
dłuższa od krawędzi podstawy. Oblicz objętość graniastosłupa i pole przekroju przechodzącego
przez wysokości podstaw i krawędź boczną. Wyznacz cosinus kąta nachylenia przekątnej ściany
bocznej do sąsiedniej ściany bocznej.
2.W czworokątnym ostroslupie prawidłowym kąt dwuścienny między sąsiednimi ścianami bocznymi
ostrosłupa jest rowny 150. Wyznacz sinus kąta ściany bocznej ostrosłupa przy podstawie.
3.W stożek o wysokości 5 dm wpisano walec wten sposób, że dolna podstawa walca zawiera się w
podstawie stożka a okrąg górnej podstawy walca zawiera się w powierzchni bocznej stożka.
Objętość walca wynosi 16π dm3, a przekrój osiowy walca jest kwadratem.. Oblicz:
a)długość wysokości i promienia walca
b)objętość stożka
c)cosinus kąta rozwarcia stożka
Dziękuję
1.Pole graniastosłupa prawidlowego trójkątnego jest równe 2{3}+24 cm2. Wysokość jest 2 razy
dłuższa od krawędzi podstawy. Oblicz objętość graniastosłupa i pole przekroju przechodzącego
przez wysokości podstaw i krawędź boczną. Wyznacz cosinus kąta nachylenia przekątnej ściany
bocznej do sąsiedniej ściany bocznej.
2.W czworokątnym ostroslupie prawidłowym kąt dwuścienny między sąsiednimi ścianami bocznymi
ostrosłupa jest rowny 150. Wyznacz sinus kąta ściany bocznej ostrosłupa przy podstawie.
3.W stożek o wysokości 5 dm wpisano walec wten sposób, że dolna podstawa walca zawiera się w
podstawie stożka a okrąg górnej podstawy walca zawiera się w powierzchni bocznej stożka.
Objętość walca wynosi 16π dm3, a przekrój osiowy walca jest kwadratem.. Oblicz:
a)długość wysokości i promienia walca
b)objętość stożka
c)cosinus kąta rozwarcia stożka
Dziękuję 




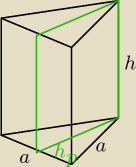 h = 2a
h = 2a
| a2√3 | a2√3 | |||
Pc = | + 3ah = | + 6a2 = 2√3 + 24
| ||
| 2 | 2 |
| a√3 | ||
hp = | =
| |
| 2 |
| a2√3 | ||
V = | * h =
| |
| 4 |
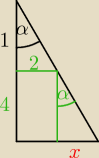 3. b)
z podobienstwa
1/2=4/x
x=8
R=2 + 8 = 10
Vs=1/3 * H * π R2
Vs= 1/3 * 5 * π * 100
3. b)
z podobienstwa
1/2=4/x
x=8
R=2 + 8 = 10
Vs=1/3 * H * π R2
Vs= 1/3 * 5 * π * 100
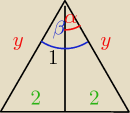 c)
z pitagorasa
y = √5
z twierdzenia cosinusow
42 = y2 + y2 + 2*y*y*cosβ
16 = 5 + 5 + 2* 5 * cosβ
10 cosβ = 6
cosβ = 0,6
c)
z pitagorasa
y = √5
z twierdzenia cosinusow
42 = y2 + y2 + 2*y*y*cosβ
16 = 5 + 5 + 2* 5 * cosβ
10 cosβ = 6
cosβ = 0,6








