geometria analityczna agags92: punkty A(4,−4) B(2,3) C(a,0) są współliniowe wyznacz a. Prosze o dokładny sposob rozwiazania

M:

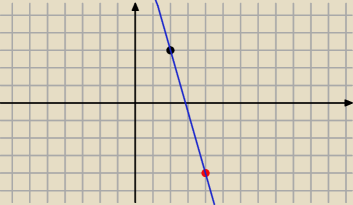
Ponury Żniwiarz : Jeśli sa współiniowe to musza leżec na jednej prostej Równanie prostej przechodzącej przez punkt A i B ma postać

	3−(−4)
y=		(x−2)+3
	2−4

	7
y=−		(x−2)+3
	2

	7
y=−		x+7+3
	2

	7
y=−		x+10
	2

Aby punkt C=(a,0) leżał ma prostej AB musi spełniac jej równanie

	7
y=−		x+10
	2

	7
0=−		*a+10
	2

7
	a=10
2

	2
a=10*
	7

	20
a=
	7

	20
Punkt C=(		,0)
	7

Jeszcze widziałem sposób na wyznacznik ale nie pamiętam

NN: Wystarczy porównać współczynniki kierunkowe ( bez pisania równań prostych

	3+4		7
aAB=		= −
	2−4		2

	4
aAC=
	a−4

	20
aAB=aAC ⇒ a=
	7

	20
C(		,0)
	7

Ponury Żniwiarz : Znalazłem to . Aby trzy punkty P₀(x₀,y₀) , P₁(x₁,y₁) ,P₂(x₂y₂) leżały na jednej prostej potrzeba i wystarcza aby punkt P₀ leżął na prostej P_P2 tzn. żeby był spełniony warunek | x₀ y₀ 1| |x₁ y₁ 1|=0 |x₂ y₂ 1| A taki wyznacznik jest łatwy do policzenia