wektory majka: Udowodnij, że jeśli w czworokącie ABCD punkty M i N są środkami przekątnych AC i BD, to MN=1/2(AB+CD) Proszę o pomoc, robię na kilka różnych sposobów ale mi nie wychodzi Chodzi oczywiście o wektory

majka: proszęęęęę!

Eta: Powinnaś poprawnie podać treść zadania, jeżeli oczekujesz poprawnej odpowiedzi ! Domyślam się ,że masz wykazać równość wektorów → → → MN = ¹₂(AB + CD) Czy mam rację ?

majka: tak

majka: napisałam, że chodzi o wektory. Dalej nie potrafię tego zrobić.

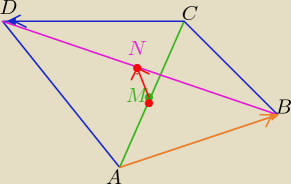
Eta: → → AB=[ x_B−x_A, y_B−y_A] CD=[x_D−x_C, y_D−y_C] → →

	xB−xA+xD−xC		yB−yA+yD−yC
12(AB+CD)= [		,		]
	2		2

	xA+xC		yA+yC		xB+xD		yB+yD
M(		,		) N(		,		)
	2		2		2		2

→

	xB+xD		xA+xC		yB+yD		yA+yC
MN= [		−		, U{		−		]
	2		2		2		2

	xB−xA+xD−xC		yB−yA+yD−yC
= [		,		]
	2		2

zatem zachodzi równość: → → → MN= ¹₂(AB+ CD)

majka: dzieki!

pigor: ... np. tak : zakładam że zrobiłaś sobie rysunek zgodnie z treścią zadania, wtedy → → → → → → → → → → → → → → → → MN= MC+CD+DN i MN=MA+AB+BN ⇔ MN=MC+CD+DN i MN= −MC+AB −DN ⇒ dodając stronami ⇔ → → → → → → → → 2MN= 0+CD+AB+0 /:2 ⇔ MN=¹₂(AB+CD) c.n.u. .

Eta: Tyż tak można