stereometria, pomocy ! tusz: Udowodnij, że pole jeśli pole jednej podstawy jest 2 razy większe od pola drugiej podstawy ostrosłupa ściętego opisanego na pewnej kuli, którego podstawami są kwadraty, to długości krawędzi jednej podstawy, średnicy tej kuli i krawędzi drugiej podstawy ostrosłupa tworzą ciąg geometryczny.

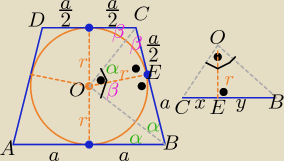
Eta: Przekrój osiowy tej bryły ( na tym rys. trapez równoramienny opisany na okręgu o pr. "r">0 2α+2β= 180^o ⇒ α+β= 180^o ⇒ ΔBOC jest prostokątny Wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostokątną na odcinki "x" i "y" tak,że h²= x*y to z tej własności mamy:

	a		a2		a√2
r2=		*a ⇒r2=		⇒ r=
	2		2		2

zatem 2r= a√2 i mamy ciąg: 2a, a√2, a ponieważ (a√2)²= 2a*a ⇒ 2a²= 2a²

	√2
zatem ciąg 2a, a√2, a jest ciągiem geometrycznym q=
	2

c.n.u.

Eta: Ciekawe zadanko

tusz: ogromne dzięki ! : D