równoległobok Bartek: Witam ! proszę o rozwiązanie zadanka ... W równoległoboku, w którym jeden z boków jest dwa razy dłuższy od drugiego, kąt ostry ma miarę 60o, a dłuższa przekątna ma długość 4 cm. a) Oblicz długości boków równoległoboku

Bartek: 60 stopni i długośc 4√7

Basia: Podpowiadam

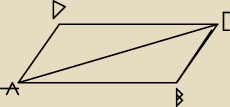
Basia: AD = BC = a AB = CD = 2a AC = 4√7 kąt BAD = 60 ⇒ kąt ABC = 120 z tw.cosinusów w tr.ABC wyliczysz a

Bartek: no właśnie robię tak i nie wychodzi. 4√7 / sin120 = 2a/sin30. Wynik jest inny niż w odp. możliwe, ze bład jest. Z tym, że ze wzorów redukcyjnych sin120 = √3/2

Basia: 1. Przekatna równoległoboku nie dzieli katów na połowy. 2. Z tw.cosinusów nie sinusów AC² = AB² + BC² − 2*AB*BC*cos120

	1
(4√7)2 = (2a)2 + a2 − 2*2a*a*(−		)
	2

112 = 4a² + a² + 2a² 7a² = 112 a² = 16 a=4 −−−−−−−−−−−−−−−−− AB = CD = 2*4 = 8 BC = AD = 4

Michuuuu: aaaaa no to chyba, że tak dzięki wielkie