Czworokąt 13LateK: kolejne mam^^ Na czworokącie ABCD, w którym AB=BC, AD= 2√3, DC=3− √3 można opisac okrąg. Wiedząc że przekatna AC ma długość 3√2, oblicz pole tego czworokata

Basia: Rysuję.

Eta: OK bo już miałam podawać wskazówki! Witam Basiu

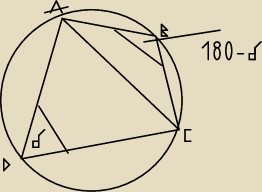Basia: Na czworokącie da się opisać okrąg ⇔ suma przeciwległych katów = 180 AD = 2√3 CD = 3−√3 AC = 3√2 z tw.cosinusów wylicz cosδ cos(180−δ) = −cosδ AB = AC = x z tw.cosinusów wylicz x

	1		1
P = PABC+PADC =		*AD*CD*sinδ +		*AB*AC*sin(180−δ)
	2		2

sin(180−δ) = sinδ sinδ wylicz z jedynki trygonometrycznej (δ<180 ⇒ sinδ>0)

Basia: Witaj Eto! Jak samopoczucie ?

Eta: OK nie narzekam, jakoś leci... Noga jeszcze mi dokucza, ale jest już lepiej niż było