 w graniastosłupie prawidłowym czworokątnym którego krawędź podstawy ma długość a połączono
środek dolnej podstawy z wierzchołkiem górnej podstawy. odcinek ten tworzy ze ściana boczną
graniastosłupa kąt o mierze α
Oblicz objętość graniastosłupa
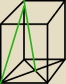
Proszę o pomoc. Czy dobrze zaznaczyłam ten kąt na rysunku?
w graniastosłupie prawidłowym czworokątnym którego krawędź podstawy ma długość a połączono
środek dolnej podstawy z wierzchołkiem górnej podstawy. odcinek ten tworzy ze ściana boczną
graniastosłupa kąt o mierze α
Oblicz objętość graniastosłupa
Proszę o pomoc. Czy dobrze zaznaczyłam ten kąt na rysunku?
 .
.
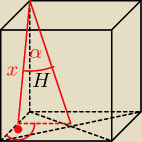 Ajtek, tak nie może być. Kąt midzy odcinkiem a paszczyzną to kąt między tym odcinkiem a
rzutem prostokątnym tego odcinka na daną płaszczyznę. Trzeba więc zrobić rzut odcinka na
ścianę boczną.
Tak powinien wyglądać rysunek.
Wskazówka: z tangensa (tgα) oblicz x, a potem mając x z Pitagorasa oblicz wysokość H, oblicz
pole podstawy (kwadrat) i wspaw do wzoru na objętość: V=Pp*H.
Ajtek, tak nie może być. Kąt midzy odcinkiem a paszczyzną to kąt między tym odcinkiem a
rzutem prostokątnym tego odcinka na daną płaszczyznę. Trzeba więc zrobić rzut odcinka na
ścianę boczną.
Tak powinien wyglądać rysunek.
Wskazówka: z tangensa (tgα) oblicz x, a potem mając x z Pitagorasa oblicz wysokość H, oblicz
pole podstawy (kwadrat) i wspaw do wzoru na objętość: V=Pp*H.
 .
.
|
| a√2 | ||||||||||||||||
sinα = | = | = | ||||||||||||||||
| D | D | 2D |
| a√2 | ||
D = | ||
| 2sinα |
| 2a2 | ||
H2 = | − a2 | |
| 4sin2α |
| a2 | 2a2sin2x | |||
H2 = | − | (dla wygody zmieniam oznaczenie kąta na x) | ||
| 2sin2x | 2sin2x |
| a2(1−2sin2x) | ||
H2 = | ||
| 2sin2x |
| a2cos2x | ||
H2 = | /√ | |
| 2sin2x |
| a√cos2x | ||
H = | ||
| sinx√2 |
| a√cos2x | ||
V = Pp*H = a2* | ||
| sinx√2 |
| a3√cos2x | ||
V = | ||
| √2sinx |
 nie analizowałam rysunku − moja wina
nie analizowałam rysunku − moja wina

