obliczyc 3 metodami przeciwnych wspoloczynnikow podstawiania i graficzna maly1111: 3x + 2y=4 3x=2−2y 2y−1=x 6y−3x=3

tim: 3x + 2y = 4 3x = 2 − 2y 3x + 2y = 4 3x + 2y = 2 Układ sprzeczny. Nie ma po co rozwiązywać. 2y − 1 = x 6y − 3x = 2 −x + 2y = 1 −3x + 6y = 2 Również układ sprzeczny...

tim: O co chodzi?

maly1111: ale chcialbym zeby ktos to rozwiazal bo potrzebuje to do szkoly

tim: A no ok

tim: 3x + 2y = 4 3x = 2 − 2y Przerzucamy. 3x + 2y = 4 3x + 2y = 2 I METODA. 3x + 2y = 4 /*−1 3x + 2y = 2 −3X − 2Y = −4 3x + 2y = 2 −−−−−−−−−−−−−−−− 0 = −2 Układ sprzeczny. II METODA 3x + 2y = 4 / :2 3x + 2y = 2 1,5x + y = 2 y = 2 − 1,5x 3x + 2y = 2 3x + 2(2 − 1,5x) = 2 3x + 4 − 3x = 2 4 = 2 Układ sprzeczny. III METODA. 3x + 2y = 4 / :2 3x + 2y = 2 / :2 1,5x + y = 2 1,5x + y = 1 y = 2 − 1,5x y = 1 − 1,5x Rysujemy. 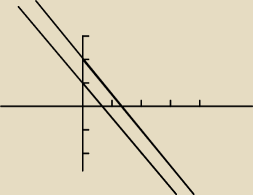Układ sprzeczny, proste są równoległe. Rysunek w nstp poście. Spróbuj drugie.

tim:

maly1111: czy w pierwwszym rysunku nie powinny sie przeciac

tim: Jak jest spreczny [nie ma rozwiązań] to jak mają się przeciąć?

maly1111: nie wiem

tim: No właśnie GGdyby się przecięły, to w niejscu przecięcia, byłoby rozwiązanie. 1195

maly1111: a drugie bo mi z tytm w ogole nie idzie

tim: Popatrz na moje i spróbuj! Potrafisz. Pisz swoje kolejne kroki. Jak będzie źle to poprawię mały

maly1111: I METODA 2y−1=x 6y−3x=3 2y−x=1/*3 6y−3x=3 6y−3x=3 6y−3x=3 0=0

maly1111: wiem gdzie jest blad powinno byc −3

tim: Świetnie

tim: Tzn powinno być −6y+3x = −3 6y − 3x = 3 −−−−−−−−−−−−− 0 = 0 Metodą przeciwnych współczynników.

maly1111: to jeszcze te 2

tim: No dawaj... Proste są

maly1111: nic mi kompletniew nie wychodzi

tim: 2y−1=x 6y−3x=3 /:3 x = 2y − 1 2y − x = 1 2y − 2y + 1 = 1 0 = 0 Układ ma nieskonczenie wiele rozwiązan.

maly1111: to jeszcze jedno tak?

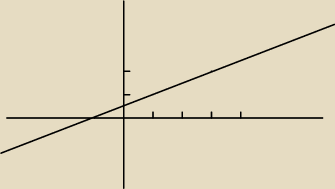
tim: Wyznaczamy y z obydwu równań: 2y − 1 = x 6y − 3x = 3 2y = x + 1 6y = 3x + 3

	x + 1
y =
	2

	3x + 3		x + 1
y =		=
	6		2

Rysujemy i wychodzi, że się nakładają, więc mają nieskończenie wiele rozwiązań.

maly1111: ok dzieki wielkie

maly1111: ok dzieki wielkie