Wyrazy w ciągu mniejsze od zera Lady_C:

	n2−12n+20
Które wyrazy ciągu o wyrazie ogólnym an=		, n∈N+ są mniejsze od zera?
	3n−14

Basia: Rozłóż licznik na czynniki liniowe (Δ, pierwiastki), a potem rozwiąż nierówność

n2−12n+20
	< 0
3n−14

ułamek < 0 ⇔ [ licznik > 0 i mianownik <0 ] lub [ licznik < 0 i mianownik > 0

tim: Hej Basiu!

Lady_C: 3n−14≠0 3n≠14

	14
n≠
	3

Lady_C: n₁=10 n₂=2

Lady_C: (n−10)(n−2)(3n−14)<0

Lady_C:

	2
n ∈(−∞,2) oraz (2		, 10)
	3

Lady_C: ale nadal nie wiem ktore wyrazy sa mniejsze od zera

Lady_C:

	14		2
aaa		to 4
	3		3

Lady_C: czyli a₁ a₅ a₆ a₇ a₈ a₉

Basia: (n−2)(n−10) > 0 ⇔ n<2 lub n>10 ⇔ n∈(−∞;2)u(10;+∞)

	14		2		2
3n−14<0 ⇔ n<		= 4		⇔ n∈(−∞;4		)
	3		3		3

szukasz części wspólnej tych przedziałów; jest to (−∞;2) stąd: n<2 czyli n=1 (bo n∈N₊)czyli tylko a₁<0 (n−2)(n−10) < 0 ⇔ n>2 i n<10 ⇔ n∈(2;10)

	14		2		2
3n−14>0 ⇔ n>		= 4		⇔ n∈(4		;+∞)
	3		3		3

	2
część wspólna to (4		;10)
	3

	2
stąd: n∈(4		; 10) czyli n=5,6,7,8,9
	3

ostatecznie: a₁,a₅,a₆,a₇,a₈,a₉ < 0

Lady_C: dziekuje za logiczne uporzadkowanie

Basia: te, których wskaźnik n spełnia nierówność czyli a₁,a₅,a₆,.....,a₉

malenka14888: a_n=n²+3_n−4

malenka14888: ktore wyrazy tego ciągu są zerowe

Alois~: a ja mam pytanko czmu sie nie rysuje tj w nierownosciach przy wielomianach bodajze tych osi ze zaznaczalam sobie 3 , 4.5 , 10 i zaczynalam od gory. tylko tak? mam wrazenie ze albo ja cos mieszam sobie albo nie wiem, pewnie pozniej sie pomyle jak bede miaala zadanie

Maslanek: Jeśli a>0, to zaczynamy od góry po prawej. Jeśli a<0, to zaczynamy od dołu po prawej

Alois~: Maslanek wiem wiem ale tutaj jakies czesci wspolne w tym zadaniu sie pojawiaja

Alois~: bo rozłożyłam sobie ze to jest (n−3)((n−10)(3n−14)<0 i ja bym wlasnie narysowala zwyczajnie os i zgodnie z tym a poleciała.

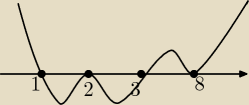
Maslanek: Powiedzmy, że masz zaznaczyć, kiedy W(x)>0 w takim przypadku. Jak to zrobisz? Swoją drogą możesz powiedzieć jakie pierwiastki jeszcze ma ten wielomian i jakiego stopnia

Alois~: to te nad osią bedą przedziały ale bez tych = 0

Alois~: znaczy bez granic jak przecina sie os bo jakos dzinwie napisalam

Alois~: bo nie rozumiem dlaczego tam wyzej w zadaniu ( bo robie takie samo) 2 odpadła chyba ze w ksiazce mam blad w odp

Maslanek: Masz źle wyznaczoną postać iloczynową (x−2)(x−10)(...)<0 Teraz już wiesz?

Alois~: oo dobrze juz przepraszam znalazłam swoj błąd

Alois~: na maturze to chyba będe za rok nawet 1+1 liczyc na kalkulatorze!