Prawdopodobieństwo TMK: Ze zbioru liczb Z={1,2,3,...,2N+1} wylosowano dwie liczby ,bez zwracania. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest liczbą parzystą. Mogę prosić o zrobienie tego na drzewkach : ) ?

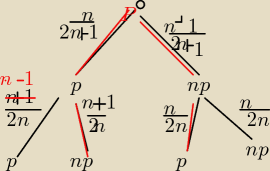
Aga1: liczb parzystych jest n, nieparzystych n+1 Suma dwóch liczb parzystych jest liczbą parzystą oraz suma dwóch liczb nieparzystych jest liczbą parzystą. Szybciej obliczyć , kiedy otrzymamy nieparzystą i skorzystać ze zdarzenia przeciwnego.

	n		n+1		n+1		1
P(A)=1−		*		−		*
	2n+1		2n		2n+1		2

TMK: .

TMK: ooooo ! Dzięki wielkie : )

Eta: @Aga1 A= {(p,p) (np,np)} na tym "krzaczku" zaznaczyłaś inaczej

TMK: Mi się wydaje że dobrze jest bo policzyłem i wyszło dobrze : )

Aga1: Na krzaczku zaznaczyłam , suma wylosowanych liczb jest liczbą nieparzystą, bo krócej. Wkurza mnie rysowanie tych krzaków.