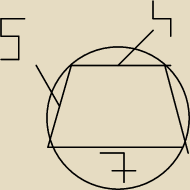
.. janek: Na rysunku obok przedstawiomo trapez wpisany w okrąg..jaki jest obwód tego trapezu

tim: Nie ma nic więcej? Może podstawa leży na średnicy?

janek: to wszystko a podstawa leży niżej niż średnica...

tim: Która klasa?

tim: Jaki dział jeszcze

janek: 2 klasa gimnazjum.,,geometria(wielokąty i okręgi)

tim: Hm... Ja też jestem w II GIM.. , ale aż muszę do książki zajrzęc

tim: A to nie jest przypadkiem, że koło jest w środku?

janek: no właśnie nie wiadomo jak tamten bok obliczyć a może on ma 5

janek: nie trapez jest wpisany w okrąg

tim: Napewno wszystko dobrze przepisałeś, narysowałeś? Rysunek jest przy zadaniu? Bo aż nie wierzę. Jakie wyd.

tim: Dobra już wiem

janek: nam to pani wydrukowała na kartce a rysunek jest przy poleceniu

Bogdan: Dzień dobry. Pytania do janka: 1. Czy na rysunku podane są wymiary boków trabezu: a = 7, b = 4, c = 5 ? 2. Jak wyznacza się obwód figury, gdy znane są długości boków tej figury?

janek: witam Bogdan a)tak b)wszystkie boki trzeba dodać

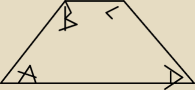
tim: Jak wiemy, kąty przeciwległe w czworokącie wpisanym w okrąg muszą dać 180^O. A także, że kąty przy tym samym ramieniu [w trapezie] mają 180^O. Katy A B C D A + B = 180 B = 180 − A B + D = 180 180 − A + D = 180 A = D A + C = 180 C + D = 180 Z tego wynika, że jest to trapez równoramienny, i ramie ma 5

Bogdan: Cześć tim Ja też nie wierzę, że ....

tim: Bogdan, ja już tak

Bogdan: No to dodaj długości boków, które masz.

janek: hehe to dobrze mówiłem ob=21

Bogdan: A co było janku trudnego w tym zadaniu?

janek: a mam jeszcze takie pytanka : a)ile osi symetri ma pięciokąt foremny,ile ośmiokąt ,a ile 27−kąt foremny b)czy na każdym rombie można opisać okrąg(wydaje mi się że nie)−

janek: nic trudnego

tim: a) Ile ma kwadrat, a ile pięciokąt for? Narysuj i policz. b) Jaki warunek musi spełniać czworokąt, żeby mógł być wpisanym w okrąg.

Bogdan: tim, przepraszam Cię, że się wtrąciłem, ale oczom nie wierzyłem, gdy zobaczyłem to zadanie. Przypominam dwa znane twierdzenia: 1.Okrąg można opisać na czworokącie wtedy, gdy sumy miar jego przeciwległych kątów są równe 180^o (α + γ = β + δ = 180^o). 2. Okrąg można wpisać w czworokąt wtedy, gdy sumy długości przeciwległych boków są równe (a + c = c + d).

tim: 1. Wiem, ale rozpisywałem jak wykorzystać 2. Nie przydatne tutaj.

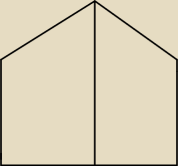
janek: a)kwadrat ma 4 osie symetri, pięciokąt ma jedną

tim: Janek odpisz: a) Ile ma kwadrat, a ile pięciokąt for? Narysuj i policz. b) Jaki warunek musi spełniać czworokąt, żeby mógł być wpisanym w okrąg. [BOGDAN PODAŁ]

janek: b)Okrąg można wpisać w czworokąt wtedy, gdy sumy długości przeciwległych boków są równe (a + c = c + d).

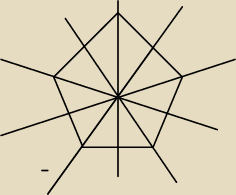
tim: a) OK. b) Pięciokąt FOREMNY Ile ma?

janek: 5...

tim: b) Może źle sformuowałem pytanie. Jaki warunek musi spełniać czworokąt, żeby można było na nim opisać koło. [czyt. wpisać czworokąt w koło]

tim: Czyli kwadrat − 4 pięciokąt − 5 Jest taka zasada, że każdy czworokąt foremny, ma tyle osi symetrii ile boków

janek: b)sumy miar jego przeciwległych kątów są równe 180o (α + γ = β + δ = 180o). ..

janek: aha

janek: czyli nie na każdym mozna opisać okrąg

Bogdan: Podałem tim te dwa twierdzenia nie ze względu na ich przydatność lub nieprzydatność w zadaniach tu zamieszczonych, ale żeby o nich gimnazjalistom przypomnieć przed rozpoczęciem działań przy podobnych zadankach.

Olcik15: Ja to mam w III