kto pomoże?? kasia.: Promień okręgu jest równy 8 a)jaką długość ma bok sześciokąta foremnego wpisanego w ten okrąg? b)jaką długość ma bok sześciokąta foremnego opisanego na tym okręgu?

kasia.:

kasia.: kto mi pomoże

Jacek Karaśkiewicz: a) Każdy z trójkątów na rysunku jest trójkątem równobocznym, jako trójkąt równoramienny o kącie przy środku okręgu równym α = 60^o. Promień okręgu i zarazem długość boku każdego z tych trójkątów wynosi 8. Jest to oczywiście długość boku sześciokąta foremnego wpisanego w ten okrąg.

kasia.: aha dzięki a przykład b

Eta: Witam Kasia! Odpowiedz na pytanie? Jak konstrukcyjnie narysować sześciokat foremnynp o boku a= 8?

Eta: Oooo , widzę ,że Jacek Karaśkiewicz już za Ciebie podał odp

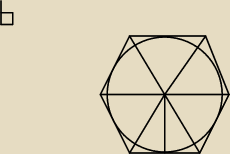
Jacek Karaśkiewicz: b) W tym przypadku promień okręgu (= 8) równy jest wysokości każdego z trójkątów tworzących sześciokąt foremny. Każdy z tych trójkątów jest trójkątem równobocznym z powodu takiego samego jak w przypadku a).

	a√3
h = 8 =		(ze wzoru na wysokość w trójkącie równobocznym)
	2

	16√3
Z tego dostajemy a =
	3

kasia.: Narysuj cyrklem dowolny okrąg o środku A, następnie na jego obwodzie oznacz dowolny punkt B, który będzie środkiem drugiego okręgu o tym samym promieniu. Punkty przecięcia się okręgów wybierz jako środki kolejnych okręgów o tym samym promieniu. Postępując analogicznie narysuj następne okręgi w ten sposób aż na obwodzie pierwszego narysowanego okręgu uzyskasz sześć punktów B, C, D, E, F, G. Otrzymane punkty połącz odcinkami. Powstałą figurę BCDEFG nazywamy sześciokątem foremnym.

kasia.: cała definicja

kasia.: dziękuje

Eta: I o to chodzi ! więc a = r = 8 w b) promień okręgu wpisanego , jak podał Ci Jacek K r= h_{Δrównobocznego} = ^a√3₂

sandrunia: nazwijcie kąty prostokąta,trojkąta,itd.. plisss........

;/: zal mi was