parametry f.kwadratowej 176x176: Mam problem z pewnym zadaniem: Dla jakich wartości parametru m (m ∊ R)suma odwrotności pierwiastków równania x²+(2−3m)x+(2m²−5m−3)=0 jest liczbą dodatnią? W odpowiedziach są przedziały (−1/2;2/3)∪(3;∞)

176x176: PS ogólnie to nie wiem skąd te przedziały się pobrały

Baś: Ech... {Δ≥0 (żeby były pierwiastki)

	1		1		x1+x2		−b   a
{		+		>0		>0		>0
	x1		x2		x1*x2		c   a

	−b
czyli ostatecznie:		>0
	c

Podstaw , wylicz, część wspólna obu warunków.

176x176: tak własnie zrobiłem i wyszło mi z

	−b		−2+3m		2
		−>		>0 czyli m>
	c		2m2−5m−3		3

	1
z delty natomiast		>0 i 3>0
	2

tylko nie potrafię tego zsumować

Baś: Czekaj. Jak wyszło Ci z delty?

176x176: 2m²−5m−3

	1
i tutaj wyszło m1= −		i m2=3
	2

czyli z odpowiedziami coś sie zgadza

Baś: z delty wychodzi Ci więc:

	1
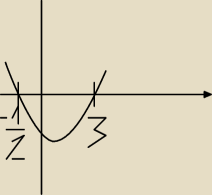
m∊(−∞, −		>∪<3,+∞) [wynika z narysowanej parabolki o a>0, i szukamy tam gdzie ≥0)
	2

Baś: i uwzględniając warunek pierwszy.... ostatecznie byłoby: m∊<3,+∞) Aczkolwiek warunek pierwszy jest niemal na 100% źle policzony. Licz jeszcze raz

176x176:

	2
a jak złączyć to m>		, aby wyszła suma z tego wszystkiego?
	3

176x176: raczej jest dobrze...bo liczby te same co w odpowiedziach

176x176: bo ztego całego równania delta wychodz 0 a tego mianownika juz jest ok

Baś: Ech... nie rozumiem ani słowa. Ale wiesz... , to że masz podobne liczby w odpowiedziach, to nic nie znaczy, bo wynik wychodzi CI całkiem inny.

	−b
dla warunku		>0
	c

	1		2
wychodzi: m∊(−		,		)∪(3,+∞)
	2		3

Lekka różnica jest... , jak mówię, ze jest źle, to jest źle.

176x176:

	−b
w takim razie jak obliczyć m należące do tego przedziału z warunku		?
	c

	2
bo mi cały czas wychodzi m>		ponieważ chce się pozbyc mianownika
	3

Baś: To jest nierówność wielomianowa. Tam się "nie pozbywasz", ten mianownik jest cholernie ważny. Zapamiętaj.

176x176: tak myślałem, tylko że wielomiany jeszcze przede mną. I głowię się jak to zrobić

Baś: Więc: nie jesteś w stanie z obecną wiedzą. Ogólnie.... mnożysz sobie tę całą nierówność * mianownik ² ten mianownik pojawia CI się w liczniku. Rozkładasz to wtedy na postać czynnikową. Korzystasz z takiego wykresiątka pomocniczego, które pozwoli CI określić znak wielomianu. Stąd wypisujesz przedziały

176x176: Spróbuję tak zrobić. Dzięki wielkie

Baś: http://www.youtube.com/watch?v=WvJc-PFKCIY

Baś: Zaczęłam to oglądać... z tego, to nawet ja nic nie rozumiem w takim zwolnionym tempie. Pacz to: http://www.youtube.com/watch?v=sXMUYmlffNA